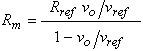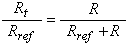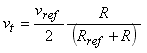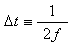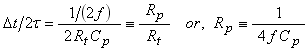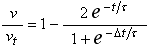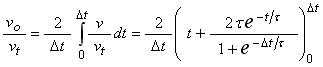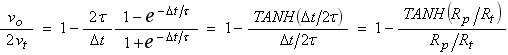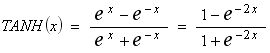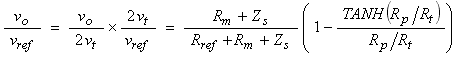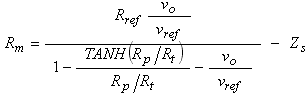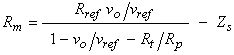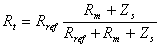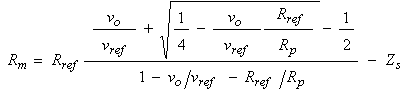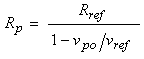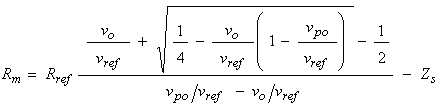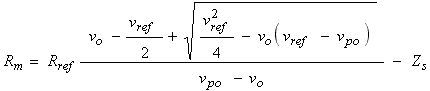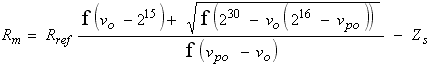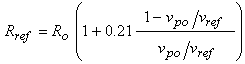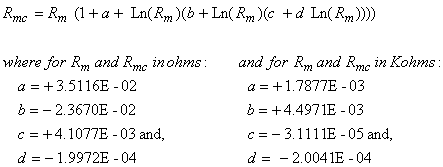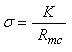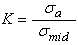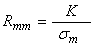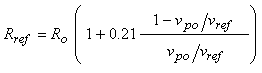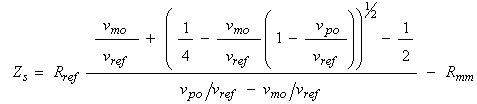Driver Software Equations
A derivation of the equations implemented by the conductivity sensing software drivers
This page describes the computations performed by the Conductivity Sensing Wildcard's software drivers. Those computations convert the voltage output of the Wildcard into an indication of the conductance/conductivity of the solution sampled by a conductivity probe/electrode.
However, if you use the board as a stand-alone instrument, and read its output voltage with a precision voltmeter, you will need to do the computations yourself. To make that easier, we provide an Excel spreadsheet that allows you to enter calibration data and the measured voltage, and computes the conductivity for you. While you may use that spreadsheet without a detailed understanding of how the computations are done, it helps to have a basic understanding. If you want to measure the output of the Conductivity Sensing Wildcard with an A/D or other embedded computer, you'll need to implement these equations in code on another processor.
Measuring resistance/conductance using a voltage divider
The Conductivity Sensing Wildcard uses a simple voltage divider network to measure the resistance of a solution between the electrodes of the conductivity sensor. The measurement resistance is just the inverse of the conductance to be measured, that is, Rm = 1/Gm. In essence, the circuit is like that of a simple voltage divider:
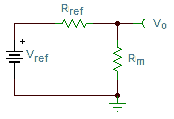
Knowing the value of the reference resistor, Rref, the unknown resistance being measured, Rm, is computed from the measured output voltage, vo, as,
The value of the reference resistor sets the middle point of the measurement range. We use a reference resistor of 1000 ohms, setting the midpoint of the measurement range to 1 mS (milliSiemen), assuming a conductivity cell constant near unity (K=1).
While the principle is simple, the Wildcard must take into account numerous subtleties. Most importantly, a DC voltage can not be used – instead a small AC voltage prevents electrode polarization and electrolysis of the solution. The AC voltage must then be precisely rectified, or demodulated, to determine its magnitude.
The following is a simplified schematic of the Wildcard's measurement circuitry and its connection to the conductivity probe:
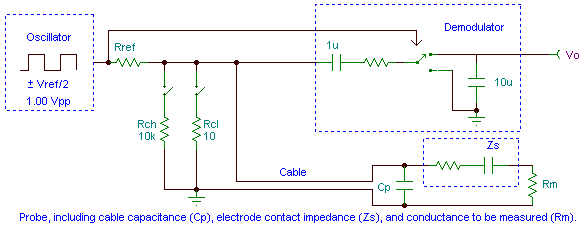
As you can see, the circuit remains essentially a voltage divider. A precision square wave of ±0.5 V is applied to a series combination of a reference resistor (nominally 1 KΩ for a midrange conductance measurement of 1 mS) and the conductance to be measured, which is indicated as the resistor at the end of the probe, Rm (ignoring for the moment the other components). The voltage at the junction of the two resistors is synchronously demodulated to determine its magnitude, from which the unknown conductance is computed.
The circuit also shows two on-board calibration resistors, used in testing or to verify the board's operation. Rch (calibration high) is sized at 10 KΩ and Rcl (calibration low) is 10 ohms. For time-of-manufacture testing they are switched into the circuit by installing jumpers.
The measurement is complicated by several factors, represented by the other components in the schematic, each of which must be compensated with parameters determined by calibration. Let me describe these factors, and the calibration procedures they necessitate, in more detail:
Tare or zero calibration
The cable, and the board itself to a much lesser degree, introduces capacitance, represented by Cp in the schematic, that limits the accuracy of low conductance measurements unless it is compensated for. The degree of its influence depends on the frequency of operation of the board, which varies a little board to board, and very much on the value of Cp. Cp arises from the cable used and its length, and so varies from cable to cable. Even when the probe is not immersed in a liquid, some current flows through the capacitance, causing a residual conductance. A zero conductance, or tare, calibration is therefore needed. This calibration should be done with the cable and probe connected, but not immersed in a fluid. Once calibrated, the Cp of a board/cable combination should not change with time, so the calibration should need to be done only once, or only before attempting precise measurements of low conductivity. For measuring moderate conductivities the calibration will not need to be repeated. As the cable capacitance influences the measurements at the low end of the conductance scale, a missing tare calibration affects only low conductance readings; mid-range or high conductance readings are not affected much. In short:
- Tare calibration is needed for accurate low conductivity measurements.
- A procedure for tare calibration should be available to the end user so that they can calibrate after changing probes or before precise measurements of low conductivity.
Full scale calibration
The conductance sensor does not contact the solution to be measured perfectly, but has a series impedance, represented by Zs in the schematic. The series impedance arises from the capacitance and conductance of the microscopic electrical double layer of charge on the electrode surface. For probe electrodes with a very high microscopic surface area the series impedance is low, and doesn't affect readings much. But for less nearly ideal probes the finite series impedance adds to the solution resistance measured and so affects high conductance readings. Mid-range and low conductivities represent much higher resistance, so adding a little additional series impedance doesn't affect them much. We don't yet know to what extent this series impedance varies from probe to probe or over time, but for accurate high conductivity measurements it must be accounted for. The full scale calibration must be performed by immersing the probe in a solution of high conductivity. Once a probe is calibrated the full scale calibration will not need to be repeated. (Although, if a probe is used over a long period of time, or if it is used in a caustic solution, electrode reactions may change its impedance.) Consequently, full scale calibration may be done at time-of-manufacture of the probe/sensor, and the resulting calibration parameter should follow the probe/sensor.
- Full scale calibration must be done for each sensor.
- A procedure for full scale calibration should be embedded in the instrument, but not generally accessible to the end user.
- A user should be able to input the full-scale calibration parameter, Zs, so it can be updated if needed when a probe is changed.
Calibration of the conductivity probe's cell constant
Mid-range conductances are measured by the board with a very high inherent accuracy. However, the conversion of the measured conductance to the solution conductivity depends on a geometrical scale factor, also called the cell constant K, of the sensor probe. Consequently, the scale factor must be determined for each probe/sensor (assuming the geometry changes a bit from probe to probe). If the sensors are sufficiently reproducible, a single K value may be used for all of them. In the most general case, you may not know how much K might vary from probe to probe. So, a calibration procedure may be used to determine K. This calibration is done by immersing the probe in a solution of mid-range conductivity and performing a measurement. Again, if you are manufacturing an end-user instrument, this is a time-of-manufacture procedure that the end user should not need to perform. Because the cell constant is purely a geometrical factor, once the cell constant is determined for a probe, it does not change with aging of the probe.
- Cell constant calibration must be done for each sensor.
- A procedure for cell constant calibration should be embedded in the instrument, but not generally accessible to the end user.
- A user should be able to input the cell constant, K, so it can be updated if needed when a probe is replaced with one of a different cell constant.
Compensation for demodulator nonlinearities
The demodulator on the Conductance Sensing Wildcard was designed to allow precision readings with less than 0.1% error over a wide conductance range. However, after its design the board was modified to operate at greater frequencies (at about 40 KHz rather than 1 KHz)1) to allow reading sensors with poor electrode impedance. Unfortunately, demodulator errors are frequency dependent, and increased 40x, to the 2-4% error range. Even so, the nonlinearities of the demodulator can be compensated with correction factors to remove virtually all of the error, as described later in this document.
Deriving the calibration equations
We'll now derive some measurement equations that ultimately will enable us to convert measured A/D counts into solution conductivity, while taking into account the three calibration parameters (the tare conductance/resistance, the full scale conductance/resistance, and the cell constant).
Referring to the above schematic, we measure the solution resistance by measuring the average demodulated output of the circuit, vo, as a portion of the reference voltage, vref. The reference will be applied to the A/D reference so that vo is measured as a number of counts from 0 to 65535, corresponding to a voltage from zero to just less than vref. The counts should be divided by 65536 to produce a floating point number between zero and one.
To derive the calibration equations we'll assume that the sensor's series impedance, Zs in the schematic, appears resistive. While in fact the impedance is a series combination of the electrode's electrical double layer capacitance, electrode spreading resistance and wire/contact resistance, owing to the synchronous detection/demodulation method used, its influence is, to a first approximation, equivalent to a simple series resistance.
In analyzing the above circuit so that we can understand how the cable capacitance influences the output, we'll combine the reference resistor and measurement resistor into a single Thevenin source impedance, driven by a Thevenin voltage.
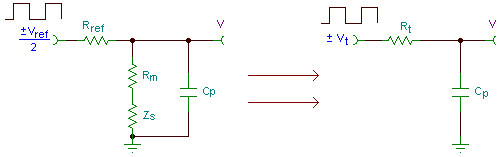
Rt and vt are related to the measurement and reference resistances as,
where R = Rm + Zs for probe measurements, or R=Rcl or R=Rch for calibration jumpers, and,
During each half cycle of the drive waveform the voltage across the cable capacitance follows an exponential decay trajectory. At the end of each half cycle, the capacitor voltage reaches its maximum excursion, v', given by,
in which Δt is the duration of one half cycle of the AC waveform; that is,
where f is the frequency of operation.
Note that the effective parallel impedance presented by the capacitor, which we'll call Rp, can be represented as,
The demodulator averages half cycles of vo, inverting alternate half cycles and summing positive halves with the inverted negative halves. Within each half cycle the voltage waveform as a function of time is given by,
Note that at t = ±Δt, this expression gives Equation 4, with v = ±v'.
The output of the demodulator is the average of the positive and negative half cycles, or,
where the expression on the right is evaluated over the interval from t = 0 to t = Δt,
or
Note that the TANH() function is the hyperbolic tangent function. As we will see, we won’t really need it, as we’ll use a simple approximation. If we did need it, and it was not available as a library function, exponential functions could be used, as,
Let's recast Equation 8 in terms of the quantity actually measured by the A/D, that is vo/vref, which is related to vo/(2vt) as,
from which we can compute Rm as,
The TANH() function is a bit intimidating, but for Rp/Rt > 4 it becomes unity to within better than 0.1%. As Rp/Rt > Rp/Rref (since Rt is always less than Rref), and Rp/Rref is likely to be greater than 4 for even long cables, we can use the approximation. (Actually, a typical 12 foot long cable may have Rp/Rref >7.) Consequently, we can approximate Equation 11 as,
which is much easier to compute.
This equation is a little deceptive, because Rm doesn’t appear just on the left side of the equation, but it also appears implicitly on the right side, embedded within Rt. From Equation 2 above, Rt is given by,
Because Equations 12 and 13 depend on each other, to solve them you can combine them and solve the resulting quadratic equation, or they can be solved iteratively. Solving the quadratic equation, Equations 12 and 13 are combined and solved for Rm as,
There is one parameter in the equation, Rp, that we can relate to a calibration condition, vpo. When a probe is plugged in, but not immersed in a solution, Rm is effectively infinite. Solving the above equation for Rp in the limit of infinite Rm yields,
In which vpo is the measurement of the board’s output when a probe is connected but not immersed in solution. Substituting Rp into Equation 14 produces the equation we’ll use to calculating the unknown resistance, Rm, as,
This equation allows us to compute the resistance of the solution given the voltage output of the board, vo, and several calibration parameters including the probe’s tare output, vpo, and series impedance, Zs. Simplifying the fraction allows us to cast it into a form more amenable to integer arithmetic, as,
We'll consider the case of using the board with a 16-bit A/D, which uses vref as its full scale reference voltage (i.e., vref is represented as 216=65536). In that case, the measured voltages are represented as a fraction of vref as 16-bit unsigned integers. If we let f() represent casting from integer representation to floating point representation, then the calculation of Equation 16b can be implemented as,
Equation 16c poses only a minor computational hazard if data acquisition errors when reading low conductances cause the denominator to become zero or negative. Consequently, before doing the division, the denominator should be limited to positive values. If data acquisition errors cause a conversion of vo greater or equal to vpo, then the computation should return zero conductance or infinite resistance2). There are no other hazards; for all vo < vpo the argument of the square root function is always positive.
Despite its seeming complexity, the above equation essentially remains the voltage divider equation, just a bit ornamented. Note that if the cable capacitance can be neglected (that is, Rp is very large and vpo becomes vref), and the sensor's series impedance is neglected (that is, Zs is very small), then Equation 16 simplifies to the voltage divider equation we started with (Equation 1),
Using other full scale values for A/D conversion
In the above derivation we assumed that a 16-bit A/D converter uses as its reference voltage the reference voltage of the board, vref, which is nominally 1.00 V. The output of the board is then measured as a fraction of that reference voltage and represented as a number in the range of 0-65535.
However, if another voltage measurement method is used that does not use the Conductivity Wildcard's reference voltage as the reference for a 16-bit conversion, the result should simply be mapped into the range in which 216 represents the full-scale reference voltage.
In the case in which the Conductivity Wildcard's reference voltage is measured with a 16-bit ADC as an integer number of counts vref', any further measurement taken with the same ADC would thus be scaled by a factor equal to 216/vref', which can be accomplished using integer arithmetic by shifting the 16-bit measurement into the upper word of a 32-bit integer, adding half of vref' for proper rounding, and dividing by vref'.
Corrections for nonlinearities
Owing to phase errors when there is appreciable cable capacitance, there are some small nonlinearities in the output of the demodulator. These nonlinearities can be compensated with two correction factors. The first correction accounts for the demodulator’s phase sensitivity, and requires that the value of Rref be modified. Instead of simply using a value equal to the onboard resistance, which we'll call Ro, we use a slightly inflated value based on the actual voltage output of the board, as,
The parameter, 0.21, was found empirically to produce the least error over a wide measurement range (30 μS to 100 mS) and for many boards. Ro is the onboard reference resistor of value 1000 ohms. This value of Rref should then be used in Equation 16 when computing the resistance Rm.
The second correction removes residual nonlinearities. After the resistance is computed, it is corrected as,
in which the Ln(Rm) represents the natural logarithm of the computed resistance. This equation reduces integral nonlinearity errors over the resistance range from about ±0.5% to ±0.1%. The coefficients of the polynomial terms were found empirically to best fit the data over 10 boards (20 channels) and a conductance range of 10 μS to 500 mS.
The correction factor of Equation 18, (that is, the quantity that multiplies Rm) happens to cross unity at Rm = 10 ohms. Consequently, some computations can be saved when doing a full scale calibration if a value of liquid conductance of 100 mS is used (if K=1).
Computing conductance in normal operation
In normal operation, A/D readings are taken to quantify vo/vref. As vref is used as the reference voltage for the A/D, the A/D counts are simply divided by the A/D’s full scale counts (65536) to get vo/vref as a floating point number between 0 and 1.
Rref is computed using Equation 17 (this needs to be done only once, at the time of tare calibration), Rm is computed from Equation 16, and it is corrected using Equation 18.
The liquid conductivity is then computed from its resistance using the cell constant as a proportionality constant, as,
in which K is the cell constant in cm-1. If Rmc is in kohms, σ is in mS/cm. If the instrument’s output will be generally expressed in mS, then it is most convenient to always express Rref, Rm and Rmc in kohms.
To summarize, we compute the conductivity by implementing Equations 16, 17, 18, and 19, in that order. These equations provide the conductivity in terms of the following:
- The measured voltage, vo, as a portion of the A/D converter's reference voltage, vref.
- A highly accurate fixed internal reference resistor, Ro, of 1000 ohms.
- And three calibration parameters, vpo/vref, Zs, and K. Of these, vpo/vref is found by doing a tare (zero scale) calibration with the probe connected but not immersed in solution, and Zs and K are found at the time of manufacture and assigned to the specific probe.
Computing the calibration coefficients
Before conductances can be computed, the three calibration coefficients must be determined. Here’s how to do it:
Tare calibration - finding the cable leakage conductance
The calibration coefficient vpo/vref represents the influence of the cable capacitance as well as any small stray on-board capacitance. It can be thought of as representing a stray, or leakage, conductance as the AC current leaks through the cable capacitance. So, before placing the probe in a solution there will be a little leakage conductance. Ideally, the leakage conductance should be small, and vpo/vref should be nearly unity; as the leakage conductance or cable capacitance increases, vpo/vref is reduced. As it will vary from board to board and from cable/probe to cable/probe, we should calibrate it when a new cable/probe is connected to an instrument.
To find it, the cable/probe should be installed but not immersed in any solution, and a calibrate button pressed. A measurement is then performed to quantify vo. We'll call this value of vo with the cable connected but the probe not contacting solution, vpo. Because we use vref as the A/D reference voltage, we need only to divide the A/D counts by 65536 to obtain vpo/vref as a floating point number between zero and one. A typical value may be around 0.85 for a long (10 to 12 foot, or 3 m) cable.
At this time, Rref should be computed using Equation 17.
The vpo/vref and Rref found should be stored in nonvolatile memory so they can be used in subsequent conductance computations. The other calibration coefficients, Zs and K, are not used in finding vpo/vref, so vpo/vref should be the first calibration coefficient computed.
Finding the cell constant, K
The cell constant of the conductivity probe is found by measuring a known solution of moderate conductivity. I suggest a solution of 1 mS. That is small enough that errors caused by an as yet unknown Zs are small (an average Zs may be used), yet it is in the range of the best accuracy for the instrument.
Let's call the measured output voltage, vmid, (for mid-range). To find K, first assume a K=1 and compute the measured conductivity, σmid, from Equations 17, 16, 18, and 19. That is, compute the conductivity as in normal instrument operation, but assuming K=1. Then compare the measured conductivity, σmid, with the actual conductivity, σa, and compute the true K as,
Finding the sensor impedance, Zs
Zs represents the effective series resistance of an individual sensor probe. Ideally, the sensor electrodes would have a very large microscopic surface area and Zs would be zero. But, it’s likely to be several ohms. Since it is in series with the solution being measured, even an infinite conductance solution would be measured as a finite conductance. That is, when measuring high conductance solutions, the measured value would saturate at 1/Zs, and go no higher. Readings of conductance less than that would be affected too, but to a lesser degree. Much smaller conductance would not be much affected. For example, if Zs=1 ohm, its inverse is 1 S. When trying to measure a conductance of 1 S, an uncompensated reading would yield ½ S. When trying to measure a much lower conductance, say 1 mS, the reading would be influenced to the extent of only one part in one thousand. Calibration of the probe is then needed to allow it to accurately measure high conductances.
To find Zs, calibrations for vpo/vref and K must first be done. Then the probe is placed in a very conductive solution, and the A/D reading is taken. The conductivity used should be an appreciable fraction of the top end of the instrument's measurement range, that is, near full scale. We'll call the solution conductivity used σm (for maximum conductivity), and the result of the A/D reading, vmo (for output voltage under conditions of maximum conductivity). Using the known K and σm, Rm is computed using Equation 19 (which we'll call Rmm), as,
In the general case, this value should be run backwards through the correction equation, Equation 18, to produce an "uncorrected" version. However, if a conductance of 100 mS, corresponding to Rm=10 ohms is used for the full scale calibration, the correction factor (generated by Equation 18) is just unity, so we don't need to "uncorrect" the value.
Then Zs is then computed from Equations 17 and 16, as,
and,
For a good probe, Zs should be a small value, just an ohm or so. If you are using high surface area electrodes, for example a graphite or platinized probe, Zs should be less than 0.1 Ω, but if you are using a microfabricated electrode of small surface area Zs may be greater than 10 Ω.
Order of calibrations
As vpo/vref doesn’t depend on knowing K or Zs, it should be determined first. Its measurement requires plugging in the cable/probe, but no immersion in solution. The computation of K is not very sensitive to the assumed value of Zs, whereas calibrating Zs is sensitive to the value used for K. Consequently, K should be found before Zs. K is found by calibrating in a moderate conductivity solution, presumably 1 mS/cm. Then Zs should be found by measurement in a high conductance solution. As the values of K and Zs are somewhat interdependent, they can be refined by recomputing them from saved values of the Conductivity Wildcard board output from the two calibrations. Use saved outputs so that immersion in the two solutions is not needed again.
Summary
The calibration and measurement equations described here are implemented two ways:
- in the Wildcard's software drivers, which you should use if you are mating the Wildcard to an Analog I/O Wildcard and Mosaic Controller, and,
- in this Excel spreadsheet, which you will find helpful if you are using the Wildcard manually.
The following is a step-by-step procedure for calibrating a conductivity probe and using it to measure a solution's conductivity.
Calibration
Before using the board and your probe for measurement you should first calibrate it. There are three calibration coefficients that fully characterize the board and your probe/electrodes. These are:
- vpo (zero scale) – The board's output when the probe is dry (i.e., zero conductance) is used to compensate for stray capacitance on the board in in the sensor cable and probe.
- K (scale factor) – The probe's cell constant characterizes the probe's geometrical factor that relates the solutions conductivity to its measured conductance.
- Zs (full scale) – The effective series impedance of the sensor electrodes, probe, cable, and on-board isolation capacitors all affect the board's ability to accurately measure very high conductivity, and so is compensated for by this calibration coefficient.
To calibrate:
Tare calibration – measure vpo and vref
Attach your probe and electrode assembly to the board, and with the electrode dry, that is, not immersed in an electrolyte, measure the board's output voltage, vpo, and its reference voltage, vref. vpo is the tare (zero-scale) calibration coefficient.
Calculate the corrected value of Rref using Equation 17. As this correction depends only on vpo and doesn't change from measurement to measurement, you can store it with the other calibration coefficients.
Determine the cell constant, K
Immerse the conductivity probe in a solution of nominally 1 mS/cm conductivity, and measure the board's output voltage, vmid. Implementing the equations above, as described in Finding the cell constant K, compute the cell constant, or scale-factor calibration coefficient, K.
Full scale conductance calibration – measure Zs
Measure Zs, the effective series resistance of your sensing electrodes, by placing the probe in an electrolyte solution of the greatest conductance you expect to analyze, and measuring the board's output. Calculate Zs using the equations described above in Finding the sensor impedance Zs. Zs is the full-scale calibration coefficient.
Save these calibration coefficients for use later when measuring the conductance of an unknown solution.
Measurement
To measure the conductivity of a solution, do the following:
Place the probe into the solution, at the same depth and position as when the calibrations were done, and measure the board's output, vo, and its reference voltage, vref.
If the corrected Rref had not been stored at the time of calibration calculate it from Equation 17.
Using Equations 16 above (you may use any of the forms, Equations 16a, 16b, or 16c), calculate the solution resistance, Rm.
Perform the correction to the measured resistance of Equation 18.
Then, convert the resistance into conductivity using Equation 19.