Chapter 6 - Analog to Digital and Digital to Analog Conversion
Many instrument applications require the monitoring of analog signals and the generation of analog control voltages. Analog to digital (A/D) converters and digital to analog converters (DACs) can perform these functions. An A/D converter samples analog signals and converts them to digital values that can be stored, processed, or displayed. A DAC generates an analog voltage whose value is proportional to a specified digital number.
The resolution of an A/D or DAC is specified in bits. For example, an "8 bit DAC" can output any of 256 distinct analog levels; 256 equals 2 raised to the 8th power, which is the maximum number of levels representable by an 8 bit number. This chapter discusses converter resolution and accuracy in detail.
The QED Board hosts both analog to digital and digital to analog converters to address a wide variety of instrumentation and control applications. The QED Board accommodates three 8 channel analog I/O devices:
- An 8 channel 8 bit analog to digital (A/D) converter is built into the 68HC11 processor chip.
- An 8 channel 12 bit A/D converter is available as an option on the QED Board.
- An 8 channel 8 bit digital to analog converter (DAC) is available as an onboard option.
The 16 analog inputs and 8 analog outputs are brought out to the 40 pin analog connector on the QED Board; Appendix A specifies the pin assignments.
The 8 bit A/D converter is in the processor, and conversion results are returned in registers in the 68HC11. The analog inputs are connected to the PORTE pins on the processor; these can be used as digital inputs if the 8 bit A/D is disabled.
The optional 12 bit A/D converter is interfaced to the processor via the fast serial peripheral interface (SPI) as described in Chapter 5. The chip select signal for the 12-bit A/D is bit 7 of the PIA's PPB.
The optional 8 bit DAC also communicates with the processor via the SPI as described in Chapter 5. Its chip select is a memory-mapped signal generated by the onboard logic.
This chapter describes the analog I/O devices available on the QED Board, explains how to connect the converters to external signals, and details the built-in driver routines that make analog I/O easy to use. Simple code is presented to calculate measured voltages based on A/D readings and to calculate the digital values required to instruct a DAC to output a specified voltage. At the end of the chapter, sample circuitry and code is presented to convert a pair of 8 bit DACs into a high resolution DAC.
Fundamentals of A/D Converters
An analog to digital converter samples an analog signal and outputs a digital number that is proportional to the analog signal. The A/D converters on the QED Board sample input voltages and communicate the digital result to the 68HC11 processor.
The analog input signal must be within the input range of the A/D converter. On the QED Board, the lower bound of the range is equal to the voltage on VRL (voltage reference/low) and the upper bound of the allowable input range is equal to the voltage on VRH (voltage reference/high). The VRL and VRH references are brought out to the 40 pin Analog I/O connector and control the input voltage range of both the 8 bit and 12 bit A/D converters. Their default values are 0 Volts (analog ground) and 5.0 Volts (analog +5V), respectively. They can be driven to different voltages by external circuitry as described below.
The converter measures the input voltage with a certain specified resolution. The resolution is the granularity with which the measurement is performed. It can be specified as a number of bits or as a voltage increment. For example, an A/D converter with only 1 bit of resolution and a 5 Volt input range would classify all voltages from 0 to just under 2.5 Volts as the digital value 0, and voltages from 2.5 Volts to 5 Volts as the digital value 1. This converter has a resolution equal to 1 bit, which corresponds to 2.5 Volts per count.
The converter measures the input voltage with a specified accuracy. The accuracy tells how close the measured value is to the actual voltage. A typical 8 bit A/D converter is accurate to within plus or minus one least significant bit.
Determining the Resolution of an A/D Converter
The VRL and VRH analog input reference pins define the lower and upper voltages that can be converted by both the 8 bit A/D and the 12 bit A/D. The resolution depends on the input voltage range. The measurement resolution of a B-bit A/D, expressed in Volts per count, is
| Resolution = (VRH - VRL)/2B | [Volts per count] | Eqn. 6.1 |
|---|
where 2B is the number of counts that can be represented by a B-bit number. From this equation we see that resolution becomes finer (better) as B grows larger or as the reference voltage range (VRH - VRL) gets smaller. For the 8 bit A/D the resolution is
| 8 bit Resolution = (VRH - VRL)/256 | [Volts per count] | Eqn. 6.2 |
|---|
and for the 12 bit A/D the resolution is
| 12 bit Resolution = (VRH - VRL)/4096 | [Volts per count] | Eqn. 6.3 |
|---|
With the default VRL and VRH of 0 V and 5 V, respectively, the resolution of the 8 bit converter is 19.5 mV per count, and the resolution of the 12 bit converter is 1.22 mV per count. The finer resolution of the 12 bit converter combined with its higher accuracy yields a more precise measurement of the analog input.
Converting an A/D Count into Its Equivalent Voltage Reading
To convert the 8-bit count returned by the A/D converter into an equivalent voltage, use the formula
| Input Voltage = VRL + ( Count * Resolution) | Eqn. 6.4 |
|---|
Combining this with Eqn. 6.1 yields
| Input Voltage = VRL + (Count * (VRH - VRL))/2B | Eqn. 6.5 |
|---|
Initializing the Analog Converters
The 8 bit A/D is disabled after a reset or restart. Execute
A/D8.ON (--)
to enable the 8 bit A/D before performing the first conversion with the on-chip A/D.
The 8 bit A/D inputs are the PortE signals which are brought out to the Analog I/O connector (see Appendix A). To turn off the 8 bit A/D and make the PORTE pins available as digital inputs, execute
A/D8.OFF (--)
The serial peripheral interface (SPI) provides a data pathway for communications with serial devices including the onboard 12 bit A/D and 8 bit DAC. As described in the previous chapter, the SPI is a fast synchronous 4-wire serial interface implemented on PortD pins 2-5 on the 68HC11.
The SPI is disabled after a reset or restart. To turn on and initialize the SPI so that it is compatible with the 12 bit A/D and 8 bit DAC, execute
INIT.SPI (--)
This configures the 68HC11 as the SPI master, with a 1 Megabit/second data transfer rate if the processor is clocked at 8 MHz, and a 2 Megabit/second rate if the processor is clocked at 16 MHz. Data is valid on the rising leading edge of the SPI clock. You may interface other peripherals via the SPI as long as each peripheral has its own unique chip select signal.
To turn off the SPI, execute
SPI.OFF (--)
When the SPI is off, the 12 bit A/D and 8 bit DAC cannot be accessed, and PortD pins 2-5 are available as general purpose digital I/O pins.
The best general purpose initialization routine for the 12 bit A/D and 8 bit DAC is the QED-Forth word
INIT.A/D12&DAC (--)
which calls INIT.SPI and also ensures the PIA is configured with PPB as an output port so that a valid chip select signal is generated for the 12 bit A/D. This routine should be executed before using the 12 bit A/D or 8 bit DAC.
The 8 Bit A/D
The 8 bit A/D inputs are the PortE signals named PE0/AN0 through PE7/AN0 available at pins 3 through 10 on the Analog I/O connector (see Appendix A). Each analog signal is converted to a number between 0 and 255 indicating its value relative to VRL (the low voltage reference) and VRH (the high voltage reference). The default values are VRL = 0 Volts (analog ground) and VRH = 5 Volts (the analog +5 Volt supply, designated +5VAN). The exact voltage difference between VRH and VRL varies slightly from board to board; it is a good idea to measure the value on your board to obtain the most exact voltage equivalents of the measured A/D results.
You may connect circuitry to the VRL and VRH pins to drive these references to desired levels between 0 and 5 Volts. For example, in some applications it may be possible to increase the resolution of the conversion by reducing the input voltage range (VRH-VRL) as specified by Eqn. 6.2.
Motorola's data books specify some restrictions on the values of the reference signals VRL and VRH (F1 p.13-10) for the 8 bit A/D. First, VRL and VRH must be less than +5.1 Volts and greater than 0 Volts. Second, the voltage on VRL must be less than the voltage on VRH. Third, the difference between the voltages, (VRH - VRL), should be greater than 3 Volts if the converter is to meet all of its stated specifications. Also note that VRH and VRL are connected to both the 8 bit A/D and the 12 bit A/D, so changing the references affects both converters.
We can calculate the range of resolutions possible from the 8 bit A/D based on Motorola's suggested limits on VRL and VRH. Referring to Eqn. 6.2, we see that the finest resolution is
3 Volts / 256 bits = 11.7 mV/bit
and the coarsest resolution is
5.1 Volts / 256 bits = 19.9 mV/bit
This resolution is the voltage equivalent of one (least significant) bit in the A/D count. The accuracy of the 68HC11's A/D converter is plus or minus one least significant bit.
Once you have obtained a digital conversion result from the A/D, it is easy to calculate the measured voltage. With B equal to 8 bits in Eqn. 6.5, the input voltage corresponding to a given digital conversion "count" is given by
| Input Voltage = VRL + (Count * (VRH - VRL))/256 | Eqn. 6.6 |
|---|
For example, with VRL = 0 Volts, VRH = 5.0 Volts, and a measured count of 128 (one half the full scale count), the measured input voltage is
Input Voltage = 128 * 5.0 / 256 = 2.5 Volts
which is at the midpoint of the input voltage range, as expected.
Built-in Driver Routines for the 8 Bit A/D
Before using the 8-bit A/D, execute
A/D8.ON
to initialize the converter. Connect the desired analog signals to the PortE inputs available at the Analog I/O connector (see Appendix A).
Placing a channel number between 0 and 7 on the stack and executing the routine
A/D8.SAMPLE ( channel# -- result )
reads the specified 8 bit A/D channel and returns the result on the data stack. For example, we can connect an analog voltage to channel 7 (pin 3 on the analog connector, labeled PE7/AN7) and print the conversion result by executing
7 A/D8.SAMPLE .
A/D8.SAMPLE GETs and RELEASEs the resource variable named A/D8.RESOURCE which mediates access to the 8-bit A/D converter in multitasking applications (the "Multitasking" chapter in the Software Manual covers these topics in detail). Unfortunately, about 80% of the execution time of the A/D8.SAMPLE routine is devoted to the GET and RELEASE overhead. In non-multitasked applications or in applications where only one task uses the 8 bit A/D, the faster routine
(A/D8.SAMPLE) ( channel# -- result )
may be used. It acquires the A/D sample without executing GET or RELEASE, and with an 8 MHz crystal it executes in only 35 microseconds compared to 180 microseconds for A/D8.SAMPLE.
The QED-Forth routine
A/D8.MULTIPLE ( xaddr\#samples\channel# -- )
rapidly obtains a multiple number of samples from an A/D channel and stores the results as sequential bytes in memory starting at the specified extended address. If the specified xaddr is in common RAM (consult the memory map appendix in the Software Manual), the sampling frequency is approximately 40 kHz (corresponding to 25 microseconds per sample). If the specified xaddr is in paged memory, the sampling frequency is approximately 10 kHz (corresponding to 100 microseconds per sample). These sampling frequencies double if the QED Board is clocked at 16 MHz.
A/D8.MULTIPLE GETs the resource variable A/D8.RESOURCE before performing the first conversion, and RELEASEs the resource variable after performing the last conversion. The GET and RELEASE operations require about 150 microseconds to execute with an 8 MHz crystal. In non-multitasked applications or in applications where only one task uses the 8 bit A/D, the programmer may use
(A/D8.MULTIPLE) ( xaddr\#samples\channel# -- )
which does not call GET and RELEASE and thus executes more rapidly. The sampling frequency is the same as specified for A/D8.MULTIPLE, but the setup and exit time is reduced by 150 microseconds.
For example, to acquire sixteen samples from channel 7 and store them starting at address B000H\0 in common memory, execute
HEX B000 0 10 7 A/D8.MULTIPLE
To view the results as stored in memory, execute
B000 0 10 DUMP
If a stable noise-free signal is attached to the PE7/AN7 input, the acquired samples should all be equal to within 1 count.
For Experts: How To Use Additional Features of the 8 Bit A/D
The built-in driver routines for the 8 bit A/D are easy to use and address the requirements of most applications. If you wish to gain a detailed understanding of the operation of the 8 bit A/D, or need to use one of its special modes, the information in Appendix H may prove useful. For example, one of the operating modes allows the 8 bit A/D converter to continuously sample four different analog inputs in rapid succession. Appendix H describes the operation of the 68HC11's A/D and presents sample code to control the 8 bit A/D.
The 12 Bit A/D
Before using the 12 bit A/D, execute
INIT.A/D12&DAC
to initialize the SPI (serial peripheral interface) and PIA (peripheral interface adapter) which handle data transfer and chip selection, respectively. The chip select signal for the 12 bit A/D is generated by the most significant bit of peripheral port B (PPB7).
Connect the desired analog signals to the inputs which are labeled 12AN0-12AN7 on the 40 pin analog I/O connector on the QED Board (see the pin diagram in Appendix A).
The 12 bit A/D converts each analog signal to a number between 0 and 4095 indicating its value relative to VRL (the low voltage reference) and VRH (the high voltage reference). The default values are VRL = 0 Volts (analog ground) and VRH = 5 Volts (the analog +5 Volt supply, designated +5VAN). The exact voltage difference between VRH and VRL varies slightly from board to board; to assure maximum accuracy you can use a high quality digital voltmeter measure the input voltage range (VRH-VRL) on your board.
VRL and VRH are connected through onboard resistors to analog ground and analog +5 Volts, respectively; this allows you to change the references to other values. The 12 bit A/D converter requires low impedance reference voltages to achieve specified performance. Thus it is strongly recommended that the VRH and VRL pins on the 40 pin analog connector be directly connected to the desired reference voltages. To achieve a full 5 Volt conversion range, use a wire to connect VRL (pin 1 on the analog connector) to analog ground (pin 19), and use a wire to connect VRH (pin 2) to +5 VAN (pin 20).
You may also connect low-output-impedance circuitry to the VRL and VRH pins to drive these references to desired levels between 0 and 5 Volts. For example, an operational amplifier may be used to establish the desired reference voltages. According to Eqn. 6.2, reducing the input voltage range (VRH-VRL) increases the attainable resolution, and this may be useful in some applications. Please note, however, that as (VRH-VRL) is decreased, the noise and nonlinearity of the 12 bit converter increase. The data sheet for the LTC1290 A/D converter chip in Appendix F contains graphs that detail these effect. Also note that VRH and VRL are connected to both the 8 bit A/D and the 12 bit A/D, so changing the references affects both converters.
Referring to Eqn. 6.3, we see that the default resolution of the 12 bit A/D when VRL = 0 V and VRH = 5.0 Volts is
5.0 Volts / 4096 bits = 1.22 mV/bit Eqn. 6.7
This resolution is the voltage equivalent of one (least significant) bit in the A/D count. The accuracy of the 12 bit A/D converter is plus or minus one least significant bit.
Once you have obtained a digital conversion result from the A/D, it is easy to calculate the measured voltage. With B equal to 12 bits in Eqn. 6.5, the input voltage corresponding to a given digital conversion "count" is given by
| Input Voltage = VRL + (Count * (VRH - VRL))/4096 | Eqn. 6.8 |
|---|
For example, with VRL = 0 Volts, VRH = 5.0 Volts, and a measured count of 2048 (one half the full scale count), the measured input voltage is
Input Voltage = 2048 * 5.0 / 4096 = 2.5 Volts
which is at the midpoint of the input voltage range, as expected.
Built-in Driver Routines for the 12 Bit A/D
The 12 bit A/D can be configured for either single-ended or differential conversion. Single-ended conversion simply means that the specified voltage is referenced to VRL (which is typically analog ground). Differential conversion means that two signals are subtracted, and the difference in their voltages is converted to a digital number. Differential conversion is useful when common-mode background signals such as 60 Hz noise or a slowly varying bias voltage must be canceled.
The 8 channels of the A/D are numbered 0...7, and are arranged in "channel pairs" as [0,1], [2,3], [4,5], and [6,7]. The members of a channel pair may be differenced to obtain a differential conversion. Moreover, either member of the pair may be specified as the "positive" side of the differential conversion.
Placing a flag (true for single-ended, false for differential) and a channel number between 0 and 7 on the stack and executing the routine
A/D12.SAMPLE ( single.ended?\channel# -- result ))
performs a 12 bit A/D conversion and returns the result on the data stack. For example, to perform a single-ended conversion (that is, referenced to VRL) of a voltage connected to channel 6 (pin 12, named 12AN6 on the analog I/O connector), execute
TRUE 6 A/D12.SAMPLE
and the result appears on the stack. You can print the result with the . (dot) command. If the input voltage equals VRL, the result will equal 0. If the input is within 1 bit of VRH, the result will equal the full-scale value of 4095. If the input is exactly half of (VRH - VRL), the result should equal 2048.
If differential conversion is specified, the channel number indicates the "positive" channel in the pair to be differenced. For example, executing
FALSE 0 A/D12.SAMPLE
converts the difference of channel 0 minus channel 1. On the other hand, executing
FALSE 1 A/D12.SAMPLE
converts the difference of channel 1 minus channel 0. Voltage differences that are negative return a result of 0.
A/D12.SAMPLE GETs and RELEASEs the resource variable SPI.RESOURCE which mediates access to the 12 bit A/D converter and the 8 bit DAC in multitasking applications. Unfortunately, about 50% of the execution time of the A/D12.SAMPLE routine is devoted to the GET and RELEASE overhead. In non-multitasked applications or in applications where only one task uses the SPI, the faster routine
(A/D12.SAMPLE) ( single.ended?\channel# -- result )
may be used. It acquires the A/D sample without executing GET or RELEASE, and with an 8 MHz crystal it executes in only 145 microseconds compared to 285 microseconds for A/D12.SAMPLE.
The QED-Forth routine
A/D12.MULTIPLE ( xaddr\#samples\single.ended?\channel# -- )
rapidly obtains a specified number of samples from an A/D channel and stores the results as sequential 2-byte values in memory starting at the specified extended address. If the xaddr is in common RAM (consult the memory map appendix in the Software Manual), the sampling frequency is approximately 12.5 kHz (corresponding to 80 microseconds per sample). If the specified xaddr is in paged memory, the sampling frequency is approximately 6.6 kHz (corresponding to about 150 microseconds per sample).
A/D12.MULTIPLE GETs the resource variable SPI.RESOURCE before performing the first conversion, and RELEASEs the resource variable after performing the last conversion. The GET and RELEASE operations require about 150 microseconds to execute with an 8 MHz crystal. In non-multitasked applications or in applications where only one task uses the 12 bit A/D and the DAC, the programmer may use
(A/D12.MULTIPLE) ( xaddr\#samples\single.ended?\channel# -- )
which does not call GET and RELEASE and thus executes more rapidly. The sampling frequency is the same as specified for A/D12.MULTIPLE, but the setup and exit time is reduced by 150 microseconds.
For example, to acquire eight single-ended samples from channel 6 and store them starting at address B000H\0 in common memory, execute
HEX B000 0 8 TRUE 6 A/D12.MULTIPLE
To view the results in memory, execute
B000 0 10 DUMP
Each sample occupies two bytes in memory. If a stable noise-free signal is attached to the 12AN6 input, the acquired samples should be nearly equal.
The 8 Bit DAC Driver
Before using the 8 bit digital to analog converter (DAC), execute
INIT.A/D12&DAC
which is fully described in the Glossary. This routine initializes the SPI (serial peripheral interface) which handles data transfer with the DAC as well as with the 12 bit A/D converter, and it also initializes the PIA (peripheral interface adapter) to be compatible with the 12 bit A/D chip selection.
Multiple devices can use the SPI link as long as each device is activated by a unique chip select signal. The DAC is activated by a memory mapped chip select signal which is active at addresses 80C0H through 80FFH. This signal is generated by onboard address decoding logic, and is transparently activated by the built-in DAC driver routines described below.
Each DAC accepts a number between 0 and 255 which we'll designate as N, and outputs a voltage given by
Vout = N/128 * Vin
where Vin is the input (reference) voltage applied to the DAC. Thus Vout ranges from 0 Volts to nearly 2*Vin Volts. The maximum allowed value for Vin is 1.5 Volts, so the maximum value of Vout is nearly 3.0 Volts. Note that the output voltage of the DAC is proportional to Vin; for this reason it is called a "multiplying DAC". Vin may be a stable DC reference voltage, or it may be a time-varying analog signal. In the latter case, the DAC becomes a automated attenuator/amplifier that can take the place of potentiometers to perform volume control and other common functions.
Providing a Reference Signal to the DAC
Before using a DAC channel, you must connect a voltage source to its Vin. The signal 1.5 VREF is available as a reference voltage for the DACs. On the current (Rev 1) version of the QED Board, this 1.5 VREF signal becomes very noisy when connected to capacitive loads, and so 1.5 VREF should not be directly connected to more than one DAC input.
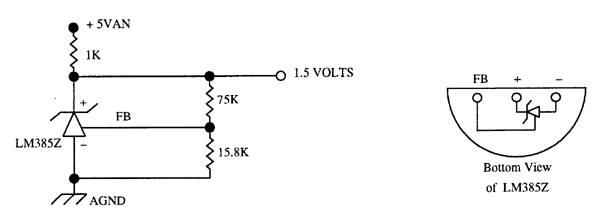
Because of the limited functionality of this reference signal, you may want to consider adding a simple circuit to provide a stable reference. We can provide purchasers of QED Product Design Kits or Developers Packages with the parts free of charge. All you need is an LM385 adjustable voltage reference chip, and three resistors as shown in Figure 6.1. The output is a temperature-stable low impedance 1.5 Volt reference signal.
Figure 6.1 This simple circuit generates a stable 1.5 Volt reference that may be connected to the Vin inputs of any or all of the 8 onboard DACs. The LM385 is a small 3-pin device that maintains 1.24V between its + and FB terminals. The 1% tolerance 75K and 15.8K resistors establish 1.5 Volts with respect to analog ground at the output. The 1K resistor provides bias current to the device. This circuit draws 3.5 mA from the +5VAN supply. The +5VAN and AGND supplies are available at the Analog I/O connector and at the power connector (see Appendix A). The bottom view of the LM385 voltage reference chip is also shown.
Built-in Driver Routines for the DAC
The 8 DAC channels are numbered 1...8; this is in keeping with the manufacturer's channel specification code. The DAC inputs (which can be reference voltages or time-varying signals) are labeled Vin1...Vin8, and the DAC outputs are labeled Vout1...Vout8 on the 40 pin analog connector. [Note: If you are interested in consulting the DAC8841 chip schematics in Appendix G, notice that the manufacturer uses alphabet characters A through H to designate DAC channels 1 through 8.]
To test a DAC channel, connect a 1.5 Volt reference (either the onboard 1.5VREF signal or the reference described in Figure 6.1) to the DAC's Vin to provide a stable reference. Then write an 8 bit value to the DAC by placing a count and channel number on the data stack and executing
>DAC ( byte\channel# -- )
For example, to set DAC1 to its midpoint value of 1.5 Volts, connect a 1.5 Volt reference to Vin1 (pin 21 on the 40 pin analog I/O connector) and execute
DECIMAL 128 1 >DAC
You can now measure the output voltage of 1.5 Volts at Vout1 (pin 22 on the 40 pin analog I/O connector).
>DAC GETs and RELEASEs the resource variable SPI.RESOURCE which mediates access to the 8 bit DAC and the 12 bit A/D converter in multitasking applications. Unfortunately, over half of the execution time of the >DAC routine is devoted to the GET and RELEASE overhead. In non-multitasked applications or in applications where only one task uses the SPI, the faster routine
(>DAC) ( byte\channel# -- )
may be used. It updates the DAC without executing GET or RELEASE, and with an 8 MHz crystal it executes in only 80 microseconds compared to 250 microseconds for >DAC.
How To Create a High Resolution DAC Using Two 8 Bit DACs
The QED Board hosts a high resolution analog option comprising an onboard 8 channel 8 bit digital to analog converter (DAC) and an 8 channel 12 bit analog to digital (A/D) converter. It is possible to combine a pair of DAC channels to obtain a single DAC output with higher resolution. If desired, a third DAC channel can be used to dynamically control the full-scale voltage of the high-resolution analog output. If you require high accuracy as well as high resolution, you can calibrate the circuit to 11 bits of accuracy at any given temperature by using one channel of the 12 bit A/D channel to monitor the combined DAC output.
The following discussion describes these approaches and presents two examples which operate with very similar circuitry. The first example is a simple high resolution DAC that requires only a single QED-Forth routine. The second example achieves higher accuracy and allows calibration at any time by using a 12 bit A/D channel to monitor the output of the high resolution DAC. It generates a 0 to 5 Volt analog output with 12 bits of resolution and 11 bits of accuracy, essentially matching the specifications of the onboard 12 bit A/D. Circuit schematics and associated calibration and control code listings are provided to help you implement these exciting capabilities.
Simple Circuitry Merges Two DACs To Boost Resolution
Two 8 bit digital to analog converters (DACs) can be configured to achieve more than 8 bits of resolution. This is accomplished by summing the outputs of two DACs so that one DAC (called the "coarse-adjust DAC") sets the major steps, and the other DAC (the "fine-adjust DAC") interpolates between the major steps to deliver more resolution between the coarse steps.
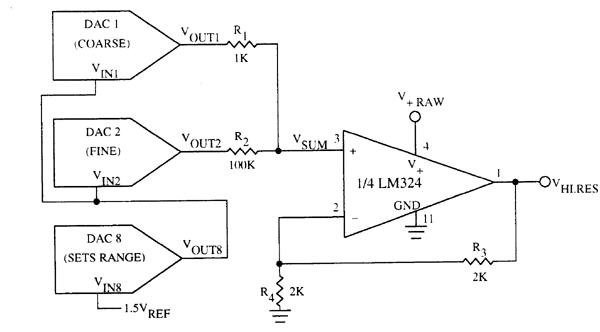
To achieve this effect, an operational amplifier (op amp) is configured as a voltage summer to add the outputs of the coarse and fine DACs as shown in Figure 6.2. DAC1 is the coarse-adjust DAC, and DAC2 is the fine-adjust DAC. DAC8 is used to set the full-scale range of DACs 1 and 2. DAC8 is optional; if control of the full-scale range is not required, Vin1 and Vin2 can be directly connected to a suitable reference such as the one illustrated in Figure 6.1.
The output of DAC1 is connected to the + input of the op amp through a 1 Kohm resistor R1, and the output of DAC2 is connected to the + input through a 100 Kohm resistor R2. The effect of DAC2 on the op amp output is 100 times (R2 divided by R1) less than the effect of DAC1. Another way of saying this is that the effective step size of DAC2 at the output of the op amp is one hundredth that of DAC1. The output of the op amp is connected to the inverting (-) input through R3, and R4 is an optional gain-setting resistor.
Figure 6.2. Schematic of a circuit that generates a high resolution analog output with adjustable full-scale range. The sum of the coarse-adjust output Vout1 and the fine-adjust output Vout2 is multiplied by 2 by the LM324 op amp to create the high resolution output Vhi.res. The output of DAC8 sets the full-scale voltage. This circuit operates from the available positive supply on the QED Board. Better accuracy and transient performance at output voltages near ground can be achieved by connecting a negative supply (such as -5 Volts) to the LM324 op amp at pin 11.
We'll name the voltage at the + input of the op amp Vsum, the output of DAC1 as Vout1, and the output of DAC2 as Vout2. Vsum is given by
Vsum = (R2*Vout1 + R1*Vout2) / (R1 + R2)
With R2 100 times larger than R1, you can see that the effect of Vout1 on Vsum is 100 times larger than the effect of Vout2.
The high resolution analog output of the op amp is labeled Vhi.res; it is related to Vsum as
Vhi.res = Vsum * ( 1 + [R3/R4] )
This equation shows the effect of the optional gain-setting resistor R4. If R4 is left out of the circuit (if its value is infinite) then the voltage gain is unity and Vhi.res equals Vsum. For finite values of R4 the gain of the amplifier circuit is
Gain = Vhi.res/Vsum = 1 + [R3/R4]
If R3 = R4 = 2 Kohms, then the voltage gain is 2; this is the gain that we illustrate with this example.
To reduce the effect of the op amp's input bias currents on the output voltage, we choose R3 and R4 such that their effective parallel resistance matches the effective parallel resistance of R1 and R2.
The LM324 quad op amp shown in the schematic is inexpensive, easy to use, and can be operated from a single or split supplies. The data sheet summary in Figure 6.3 describes the chip's characteristics and illustrates the pin connections.
Figure 6.3. Data sheet summary for the LM324 op amp, courtesy of National Semiconductor Corporation.
The schematic in Figure 6.2 shows the op amp powered by a positive supply (at pin 4 on the LM324) tied to the QED Board's V+raw and a lower supply (pin 11 on the LM324) tied to the QED Board's ground. The positive supply at pin 4 must be at least 1.5 Volts greater than the highest voltage required at the op amp's output. In some applications, noise performance may be improved by powering the op amp from a regulated voltage of 7 Volts or higher. The op amp's output can go as low as the low supply voltage (in this case ground) but for better accuracy and dynamic performance near ground, you can apply a negative supply voltage (such as -5 Volts) to pin 11 of the LM324 chip.
We use DAC8 to set the full-scale range of DAC1 and DAC2; it could also set the range of the remaining DACs. The reference input to DAC8 (Vin8) is tied to the available 1.5 Volt reference signal (either the QED Board's 1.5VRef, or better yet, the output of the circuit shown in Figure 6.1). Recall that the 1.5Vref signal cannot drive more than 1 DAC directly as described earlier in this chapter. The output of DAC8 (Vout8) is tied to Vin1 and Vin2.
A Simple DAC Control Algorithm
Let's start with a very simple algorithm that yields a high resolution DAC output. We make the following two assumptions to simplify the problem:
- While we do want high resolution, we assume that we do not need a highly accurate DAC output. Thus we can tolerate some nonlinearity and some drift in the DAC output (say, as a function of temperature variations over time). This assumption makes sense for many closed-loop control applications, or for applications where the temperature of the electronics is held fairly constant, thus minimizing drift.
- We assume that each count of DAC1 will result in a fixed change in the op amp's Vhi.res output; for the purposes of this example we choose 20 mV per coarse step.
For example, when we write a count of 200 to DAC1, we want Vhi.res to equal 4.00 Volts. Thus, to set the full-scale op amp output voltage, we can set DAC1 to 200 and DAC2 to 0 as
DECIMAL 200 1 >DAC 0 2 >DAC
and monitor the op amp's Vhi.res output with a voltmeter or with an A/D channel such as 12AN0. Now set an initial value on DAC8 as
110 8 >DAC
and adjust the DAC8 value until Vhi.res equals 4.00 Volts.
Once the full scale voltage has been set, the code in Listing 6.1 can be used to control the DAC pair with 1 milliVolt (mV) resolution over a 0 to 4 Volt range; this corresponds to approximately 12 bits of resolution.
In essence, we're performing a one-time calibration of the full-scale output by setting DAC8, and we're relying on the inherent linearity and stability of the DACs. Consequently, the typical accuracy of this scheme will be less than 12 bits and will be a function of operating temperature. In addition, monotonicity is not guaranteed by this approach. However, this simple approach provides a simple and cost-effective solution for many real world applications.
Listing 6.1. A simple routine to control the circuitry shown in Figure 6.2 to implement a functional high resolution DAC.
4 USE.PAGE \ set up memory map; you can remove this command if you have already \ specified your memory map (dictionary, names, and variable pointers). ANEW HI.RES.DAC.CODE \ define a marker to simplify re-loading the code DECIMAL \ set the number base 1 CONSTANT COARSE \ name DAC1 2 CONSTANT FINE \ name DAC2 8 CONSTANT SPAN \ name DAC8; its input is a 1.5V reference 110 CONSTANT DEFAULT.SPAN \ writing this to DAC8 yields 20mV/step 20 CONSTANT MV/STEP \ output changes 20 mV per coarse step 100 CONSTANT COARSE/FINE.RATIO \ ratio equals R2/R1 : >HI.RES.DAC ( n -- ) \ n = millivolts desired at output \ updates high resolution output to the desired voltage MV/STEP /MOD ( -- remainder\quotient ) COARSE >DAC ( -- remainder ) \ set coarse DAC COARSE/FINE.RATIO * MV/STEP / ( -- fine.count ) FINE >DAC ( -- ) \ set fine DAC ; \ To use, execute: \ INIT.A/D12&DAC DEFAULT.SPAN SPAN >DAC \ To calibrate the output, you can adjust the span count as suggested in the text. \ Then place desired {integer} output voltage in mV on the stack and call: \ >HI.RES.DAC
A Full-Featured DAC Control Algorithm
This example demonstrates how to implement a high resolution DAC whose output range, step size, accuracy and linearity specifications match those of the onboard 12 bit A/D. We combine two 8 bit DACs and an op amp, and monitor the output with one channel of the onboard 12 bit A/D. The result is a DAC with a 0 to 5 Volt output range, 12 bit resolution, 1.22 mV step size (see Eqn. 6.7), and 11 bit accuracy and linearity (see Appendix F for a description of the A/D specifications).
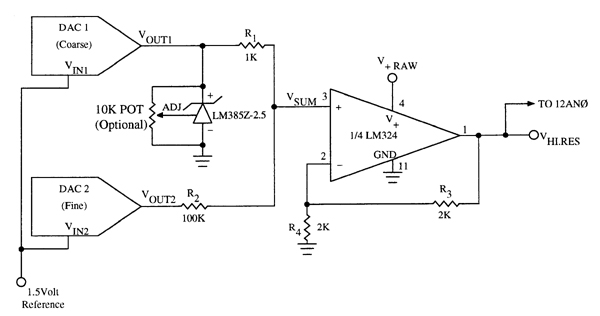
The required circuitry is shown in Figure 6.4. It is similar to the previous example circuit (Figure 6.2). Note that in Figure 6.4 the reference input to DAC1 and DAC2 is a steady 1.5 Volts; Figure 6.1 shows how to generate this reference voltage. The output of the op amp, labeled Vhi.res, is connected to a 12 bit A/D channel such as 12AN0 which is brought out to the analog I/O connector; see Appendix A for the pinouts of all of the analog I/O signals. To prevent an over-voltage condition that could damage the 12 bit A/D, the output of DAC1 is clamped to a maximum of 2.5 Volts by a reference diode. This limits the maximum voltage at Vhi.res to 5.0 Volts.
Figure 6.4. Schematic of a calibrated high resolution DAC that matches the accuracy and resolution specifications of the onboard 12 bit A/D converter.
The circuit of Figure 6.4 is the same as that of Figure 6.2, with three exceptions: First, this circuit uses a constant 1.5 Volt reference (see Figure 6.1). Second, the Vhi.res output of this circuit is connected to an input of the 12 bit A/D; the A/D is used to calibrate the combined DAC. Third, a clamping voltage reference diode is placed at the output of DAC1 to limit the maximum output at Vhi.res to about 5 Volts; this prevents damage to the 12 bit A/D. The optional potentiometer across the clamping device can be used to trim the clamp voltage to 2.5 Volts. Note that the pinout of the LM336Z-2.5 is the same as that of the LM385 shown in Figure 6.1.
The QED-Forth code for this application is simple in concept. We will create two high level routines, one that calibrates the DAC output (called CALIBRATE.12BIT.DAC) and one that writes a digital code to the DAC (called >12BIT.DAC) to update the analog output.
The calibration routine's job is to ensure that the DAC's transfer function (the relationship between its output and the digital code) exactly matches the transfer function of the 12 bit A/D. It does this by filling in a look-up table and calculating some constants. Calibration can be performed any time. This ability to recalibrate minimizes the effect of nonlinearities and temperature-induced drift in the DAC characteristics.
The routine that writes to the high resolution DAC accepts a 12 bit count and establishes the corresponding analog voltage at the output of the compound DAC. As mentioned earlier, the analog output is 1.22 mV times the specified count. This is exactly the behavior that we expect from a 12 bit DAC with a 0 to 5.0 Volt output range.
As in the previous example, this code generates a single high resolution digital-to-analog output by combining the outputs of 2 8-bit DACs. One DAC (DAC1) provides the "coarse" output, and the other (DAC2) provides the "fine" adjustment that interpolates between the coarse steps. Resistors at the outputs of the 2 DACs set a 100:1 ratio between coarse and fine voltage steps. The scaled outputs of the DACs are summed at the positive input of an operational amplifier (op amp). A feedback resistor network comprising two resistors provides a voltage gain of 2.0.
We connect the (reference) input of each DAC to a 1.5 Volt reference. Given an op amp voltage gain of 2 and the clamp that limits the output of the coarse DAC to 2.5 Volts, the maximum op amp output is about 5 Volts. We calibrate and use the 0 to 5.0 Volt range which corresponds to the range of the 12 bit A/D converter.
Listing 6.2 presents the control code. A brief overview is presented here to help put the code in perspective.
The first section of the code defines the required data structures, constants and variables. After naming the A/D and DAC channels and some useful constants, we define a look-up table named COARSE.12BIT.COUNTS that will be initialized by the calibration routine. Each entry in the table holds the 12 bit count (as measured by the onboard A/D) that corresponds to each of the steps of the coarse-adjust DAC. We define the floating point variables 12BIT.COUNTS/FINE.STEP and 12BIT.COUNTS/COARSE.STEP which will contain the average number of 12 bit counts (as measured by the A/D) for the fine-adjust DAC and coarse-adjust DAC, respectively.
During calibration of the coarse-adjust DAC, a number of 12 bit A/D readings specified by the constant #CALIBRATION.SAMPLES will be acquired and averaged. This averaging reduces the effect of random noise. The temporary array named SAMPLE.BUFFER will hold the intermediate results.
The next section of the code calibrates the coarse-adjust DAC. After setting the fine-adjust DAC to its default midpoint position, the CALIBRATE.COARSE.DAC routine places one value in the COARSE.12BIT.COUNTS look-up table for each step of the coarse-adjust DAC. It calls GET.AVG.12BIT.COUNT to perform the noise-reduction averaging. It also calculates the average number of 12 bit steps per step of the coarse-adjust DAC, and saves the result in the variable 12BIT.COUNTS/COARSE.STEP.
The next two routines calibrate the fine-adjust DAC. The routine CALIBRATE.FINE.DAC sets the coarse DAC to a default value of 128, then sets the fine DAC to a nominal "low" value of 28. It calls INC.FINE.DAC.TIL.A/D.CHANGES which increments the fine DAC until the value read by the 12 bit A/D toggles to a new count. Then the fine DAC is changed to a nominal "high" value of 228, and the process is repeated. The difference in A/D counts divided by the difference in the fine-adjust DAC counts is stored in the variable 12BIT.COUNTS/FINE.STEP.
The final section of the code defines the two high level routines. CALIBRATE.12BIT.DAC simply initializes the arrays and calls CALIBRATE.COARSE.DAC and CALIBRATE.FINE.DAC. You can execute CALIBRATE.12BIT.DAC any time. For example, you may want to execute it every time the application is initialized. Alternatively, you could recalibrate every hour, or when a significant temperature change has occurred that could cause the DAC or op amp characteristics to shift slightly. For some closed-loop or temperature-controlled applications, you may even be able to calibrate the DAC only once at compile time and save the calibration look-up table and constants as a CONSTANT.ARRAY and FCONSTANTS in PROM.
To initialize the analog converters, execute the QED-Forth routine
INIT.A/D12&DAC
Then initialize the calibration array and variables by executing
CALIBRATE.12BIT.DAC
The routine >12BIT.DAC expects a 12 bit count on the data stack, and writes to the high resolution DAC pair. For example, since 2048 is half of the full-scale 12 bit count (half of 4096), executing
2048 >12BIT.DAC
should output an analog signal of 2.500 Volts, which is half of the full-range reference voltage VRH.
With only slight modifications to the code you can implement four high resolution DACs, each comprising a pair of 8 bit DACs and an op amp.
Summary
The QED Board offers an 8 bit A/D converter and optional 12 bit A/D and 8 bit DAC. Each converter has eight channels, so you can dedicate up to 24 analog I/O lines to your application. Built-in QED-Forth device drivers configure the converters, read the A/Ds, and write to the DACs. Single and multiple A/D sampling is supported. The device drivers include resource variable calls to ensure full compatibility with multitasked systems. For programmers whose applications do not require multitasking, faster driver routines are available that do not access resource variables.
Pairs of DACs can be combined to achieve 12 bit digital to analog resolution. The presence of 12 bit digital-to-analog and analog-to-digital conversion allows the QED Board to address many high performance applications.
Listing 6.2. Control code for full-featured high resolution DAC.
\ *************** HIGH RESOLUTION DAC CONTROL CODE *************** \ ********** CONVERTS TWO 8 BIT DACS INTO A COMBINED DAC *************** \ ** CALIBRATED TO THE RESOLUTION AND ACCURACY OF THE ONBOARD 12 BIT A/D ** \ Copyright 1992, Mosaic Industries Inc. \ This code generates a single high resolution digital-to-analog output \ by combining the outputs of 2 8-bit DACs. \ One DAC provides the "coarse" output, and the other provides the "fine" \ adjustment that interpolates between the coarse steps. \ Resistors at the outputs of the 2 DACs \ set the ratio between coarse and fine voltage steps. \ In this example we combine two DACs and an op amp to yield the same \ 12 bit resolution and 0 to 5 Volt range as the 12 bit A/D. \ In other words, we are creating a single 12 bit DAC \ with a 0 to 5 Volt output range. \ We choose a 100:1 ratio between coarse and fine steps. \ DAC1 provides the coarse output, driving a 1Kohm resistor. \ DAC2 provides the fine output, driving a 100Kohm resistor. \ The ratio of the two output resistors provides \ the desired 100:1 ratio between coarse and fine steps. \ The two resistors are tied together at the positive input \ of an operational amplifier (op amp). \ A feedback resistor network comprising two resistors \ provides a voltage gain of 2.0. \ We connect the (reference) input of each DAC to a 1.5 Volt reference. \ Given an op amp gain of 2, at the maximum coarse DAC count of 255 \ the maximum op amp output is about 6 Volts. To avoid damaging the input \ of the 12 bit A/D, we clamp the output of the coarse DAC to 2.5 Volts \ with a 2.5 Volt reference diode across its output. \ We calibrate and use the 0 to 5.0 Volt range which corresponds \ to the range of the 12 bit A/D converter. DECIMAL 11 WIDTH ! 4 USE.PAGE \ set up memory map; you can remove this command if you have already \ specified your memory map (dictionary, names, and variable pointers). ANEW HI.RES.DAC.CODE \ define a marker to simplify re-loading the code \ ******* Define and Initialize Constants, Arrays and Variables *********** 0 CONSTANT A/D.CAL.CHANNEL \ channel# of 12 bit A/D used to cal 1 CONSTANT COARSE \ coarse-adjust DAC channel# 2 CONSTANT FINE \ fine-adjust DAC channel# 256 CONSTANT #8BIT.COUNTS \ = 2 to the 8th power 128 CONSTANT 8BIT.MIDPOINT \ = half of #8BIT.COUNTS 4096 CONSTANT #12BIT.COUNTS \ = 2 to the 12th power ARRAY: COARSE.12BIT.COUNTS \ This is the main look-up table, initialized at calibration time. \ It is a 1-dimensional integer array; its index is the coarse DAC count; \ its contents equal the corresponding 12 bit A/D reading. FVARIABLE 12BIT.COUNTS/FINE.STEP \ initialized at calibration time; \ holds number of 12bit a/d counts per count of the fine-adjust DAC. FVARIABLE 12BIT.COUNTS/COARSE.STEP \ initialized at calibration time; holds approximate number of \ 12bit a/d counts per count of the coarse-adjust DAC. 16 CONSTANT #CALIBRATION.SAMPLES \ This is the number of samples averaged for each coarse DAC count \ during calibration. \ This constant can be set to a number in the range 1 to 16, inclusive. \ If greater than 16, the simple integer averaging algorithm shown \ below may overflow. Less averaging gives quicker calibration; \ more averaging gives better noise reduction. ARRAY: SAMPLE.BUFFER \ a temporary buffer used during averaging; \ holds #CALIBRATION.SAMPLES readings from 12 bit A/D. : INIT.ARRAYS ( -- ) #8BIT.COUNTS 1 2 ' COARSE.12BIT.COUNTS DIMENSIONED ' COARSE.12BIT.COUNTS ZERO.ARRAY #CALIBRATION.SAMPLES 1 2 ' SAMPLE.BUFFER DIMENSIONED ' SAMPLE.BUFFER ZERO.ARRAY ; \ ********** Calibrate the Coarse-Adjust DAC ************** \ These routines fill in the look-up table named COARSE.12BIT.COUNTS \ with the 12 bit value (measured by the 12 bit A/D) \ that corresponds to each count of the coarse DAC. \ During calibration, multiple A/D readings are averaged for each DAC step \ to reduce the effect of random noise. The floating point variable \ 12BIT.COUNTS/COARSE.STEP is also initialized. : U/ROUND ( n1\n2 -- n3 | n3 = n1/n2, rounded up if necessary) \ This is an integer division routine with rounding for maximum accuracy. DUP>R \ copy & save denominator U/MOD SWAP 2* ( -- quotient\remainder*2 ) R> >= ( -- quotient\round.up? ) IF 1+ ( -- rounded.quotient ) ENDIF ; : GET.AVG.12BIT.COUNT ( -- n | n = average.a/d12.count ) \ Assumes that the output of the combined DAC has been set; \ Acquires and averages 12 bit A/D samples corresponding to the DAC output. 0 SAMPLE.BUFFER #CALIBRATION.SAMPLES TRUE A/D.CAL.CHANNEL A/D12.MULTIPLE \ places results in calibration.buffer 0 ( -- accumulator ) #CALIBRATION.SAMPLES 0 DO I SAMPLE.BUFFER @ + ( -- updated.sum ) LOOP #CALIBRATION.SAMPLES U/ROUND ( -- avg.a/d12.count ) ; : CLAMP.DAC.COUNT ( n1 -- n2 | 0 <= n2 <= 255 ) 0 MAX 255 MIN \ clamp the input to the range of the 8 bit DAC ; : CALIBRATE.COARSE.DAC ( -- ) \ initializes the COARSE.12BIT.COUNTS array to contain the \ 12 bit A/D count corresponding to each step of the coarse-adjust DAC \ while the fine-adjust DAC is in its "neutral" midpoint position. \ Then initializes the 12BIT.COUNTS/COARSE.STEP variable to contain \ the approximate number of 12 bit counts per step of the coarse-adjust dac. 8BIT.MIDPOINT FINE >DAC \ set fine DAC to its neutral position #8BIT.COUNTS 0 \ for the range of coarse DAC counts DO I COARSE >DAC ( -- ) \ set coarse DAC GET.AVG.12BIT.COUNT DUP ( -- avg.count\avg.count ) I COARSE.12BIT.COUNTS ! ( -- avg.count ) \ store result #12BIT.COUNTS 1- >= \ are we at top of A/D range? IF LEAVE \ we're done if A/D has topped out ENDIF LOOP \ now calc counts per coarse step... 8BIT.MIDPOINT COARSE.12BIT.COUNTS @ FLOT 8BIT.MIDPOINT FLOT F/ 12BIT.COUNTS/COARSE.STEP F! ; \ ********** Calibrate the Fine-Adjust DAC ************** \ These two routines initialize the floating point variable named \ 12BIT.COUNTS/FINE.STEP. Because the step size of the fine-adjust DAC \ is significantly smaller than the step size of the 12 bit A/D, \ we need to calculate this value carefully. Starting at a nominal "low" \ value, we increment the fine DAC until the 12 bit A/D reading changes; \ this establishes the fine DAC count that corresponds to an A/D transition. \ We repeat the process for a nominal "high" value of the fine-adjust DAC, \ and form the 12BIT.COUNTS/FINE.STEP ratio. : INC.FINE.DAC.TIL.A/D.CHANGES ( initial.dac.count--final.dac.count\a/d.count) \ increments the fine dac until a new 12 bit A/D count is measured. \ Returns the dac count and the corresponding 12 bit a/d count on the stack. LOCALS{ ¤t.dac.COUNT | &last.a/d.COUNT } GET.AVG.12BIT.COUNT TO &last.a/d.COUNT \ average samples to get A/D count BEGIN ¤t.dac.COUNT 1+ DUP FINE >DAC TO ¤t.dac.COUNT GET.AVG.12BIT.COUNT DUP &last.a/d.COUNT = WHILE \ keep going while A/D count is unchanged TO &last.a/d.COUNT REPEAT ( -- latest.a/d.count ) ¤t.dac.COUNT SWAP ( -- final.dac.count\final.a/d.count ) ; : CALIBRATE.FINE.DAC ( -- ) \ initializes the floating point variable 12BIT.COUNTS/FINE.STEP. \ First sets fine dac to a "low" value that just toggles the A/D, \ then sets the fine dac to a "high" value that just toggles the A/D, \ then calculates the difference in A/D readings divided by the difference \ in fine dac counts, and stores this value in 12BIT.COUNTS/FINE.STEP. LOCALS{ | &low.a/d.cnt &low.dac.cnt } 8BIT.MIDPOINT COARSE >DAC \ set coarse dac to a nominal value 28 DUP FINE >DAC \ set fine dac to a "low" count INC.FINE.DAC.TIL.A/D.CHANGES ( -- final.dac.count\final.a/d.count ) TO &low.a/d.cnt TO &low.dac.cnt ( -- ) 228 DUP FINE >DAC \ set fine dac to a "high" count INC.FINE.DAC.TIL.A/D.CHANGES ( -- hi.dac.cnt\hi.a/d.cnt ) &low.a/d.cnt - FLOT ROT &low.dac.cnt - FLOT ( -- a/d.cnt.difference\dac.cnt.difference) F/ 12BIT.COUNTS/FINE.STEP F! ( -- ) \ save result in variable ; \ ******************* High Level User Routines *********************** : CALIBRATE.12BIT.DAC ( -- ) \ initializes the COARSE.12BIT.COUNTS array, \ and the variables 12BIT.COUNTS/FINE.STEP and 12BIT.COUNTS/COARSE.STEP INIT.ARRAYS CALIBRATE.COARSE.DAC CALIBRATE.FINE.DAC ; : CALC.FINE.ADJUSTMENT ( desired.count\coarse.count -- fine.count ) \ given the desired 12bit count and the estimated coarse count, \ calculates the optimal fine adjustment count as \ 128 + (n - actual.coarse.12bit.count) / 12bit.counts.per.fine.step \ where n is the desired 12 bit count. CLAMP.DAC.COUNT COARSE.12BIT.COUNTS @ - FLOT 12BIT.COUNTS/FINE.STEP F@ F/ FIXX 8BIT.MIDPOINT + ; : >12BIT.DAC ( n -- | n = 12bit.count for 0-5Volt range ) \ writes to the "12 bit DAC" formed by the combined DACs and op amp \ Establishes the output voltage specified by the 12 bit count n. \ The calibrated output voltage range for the 12 bit DAC is 0 to 5 Volts. \ algorithm: \ 1. Set coarse count = desired.12bit.count / 12bit.counts.per.coarse.step \ 2. Look up in array the 12 bit count that corresponds to the coarse count \ 3. Set fine count = \ 128 + (n - actual.coarse.12bit.count) / 12bit.counts.per.fine.step \ where n is the desired 12 bit count. \ We allow 1 iteration step in case the fine count is outside the range 0-255. 0 MAX 4095 MIN \ clamp to allowable range LOCALS{ &desired.COUNT | &coarse.COUNT &fine.COUNT } &desired.COUNT FLOT 12BIT.COUNTS/COARSE.STEP F@ F/ FIXX CLAMP.DAC.COUNT ( -- estimated.coarse.dac.count ) TO &coarse.COUNT &desired.COUNT &coarse.COUNT CALC.FINE.ADJUSTMENT ( -- fine.dac.count) TO &fine.COUNT \ this is our first estimate &fine.COUNT 0< \ if goal is out of reach... IF &coarse.COUNT 1- TO &coarse.COUNT \ ... reduce coarse and re-calc fine &desired.COUNT &coarse.COUNT CALC.FINE.ADJUSTMENT ( -- fine.dac.count) TO &fine.COUNT ELSE &fine.COUNT 255 > \ if goal is out of reach... IF &coarse.COUNT 1+ TO &coarse.COUNT \ increase coarse, calc fine &desired.COUNT &coarse.COUNT CALC.FINE.ADJUSTMENT ( -- fine.count) TO &fine.COUNT ENDIF ENDIF &coarse.COUNT CLAMP.DAC.COUNT COARSE >DAC \ set coarse dac &fine.COUNT CLAMP.DAC.COUNT FINE >DAC \ set fine dac ; \ NOTES: \ Make sure to execute INIT.A/D12&DAC each time you run this application. \ You can then execute CALIBRATE.12BIT.DAC at any time; it takes about \ 3 seconds to execute {reduce #CALIBRATION.SAMPLES to reduce calibration time}. \ Once the calibration array and variables have been initialized \ by CALIBRATE.12BIT.DAC, simply place a 12 bit integer count on the stack \ and execute >12BIT.DAC to update the analog output.