Data Acquisition Using Analog to Digital Conversion
How to use the HCS12 MCU's 16-channel 10-bit ATD converter on the PDQ Board
This page describes the 10-bit Analog-To-Digital (ATD) inputs available on the PDQ Single Board Computer (a low cost SBC using the 9S12 HCS12 68HCS12 MC9S12DP512 MC9S12A512 microcontroller), explains how to connect the converters to external signals, and details the built-in C language software driver routines that make the analog inputs easy to use.
9S12/HCS12 ATD specifications
In brief, the features of the A/D converter on the Freescale 9S12 (HCS12) MCU are given by the following table and shown in Figure 1:
| A/D Specifications |
|---|
| 16 channels |
| 8 or 10 Bit Resolution |
| 7µsec, 10-Bit Single Conversion Time |
| Sample Buffer Amplifier |
| Programmable Sample Time |
| Left/Right Justified, Signed/Unsigned Result Data |
| External Trigger Control |
| Conversion Completion Interrupt Generation |
| Analog Input Multiplexer for 8 Analog Input Channels |
| Analog/Digital Input Pin Multiplexing |
| 1 to 8 Conversion Sequence Lengths |
| Continuous Conversion Mode |
| Multiple Channel Scans |
The HC12/9S12/HCS12 ATD subsystem comprises two 8-channel blocks, each designated ATD_10B8C by Freescale. Each block is structured as shown in the following block diagram:
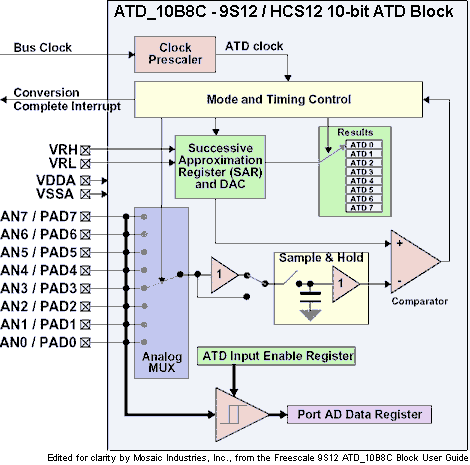
Detailed specifications are found in the Freescale 9S12 ATD_10B8C Block User Guide. You can also download here all of Freescale's MC9S12/HCS12/9S12 manuals.
Built-in software controls the 9S12/HCS12 analog inputs
Many instrument applications require monitoring of analog signals for analog data acquisition. Analog To Digital (ATD) converters can perform this function. An ATD converter samples analog signals and converts them to digital values that can be stored, processed, or displayed.
The resolution of an ATD is specified in bits. For example, an 8-bit ATD converts an analog signal into one of 256 discrete digital numbers, while a 10-bit ATD converts an analog signal into one of 1024 discrete digital numbers.
The PDQ Board hosts 16 channels of 10-bit analog to digital conversion to address a wide variety of instrumentation and control applications. The 9S12/HCS12 processor chip implements these inputs as pins AN0 through AN15 which are brought out to the Analog I/O Field Header on the PDQ Board; the connector diagrams in Appendix B: Connector Pinouts specify the pin assignments.
The ATD inputs convert unipolar signals with a nominal 0 to +5 volt range into 10-bit results. There are two ATD converter systems on the 9S12/HCS12 MCU: one implements inputs AN0 through AN7, and the other implements inputs AN8 through AN15. Each converter is controlled and configured by pre-coded driver routines in the operating system as listed in Table 11-1.
Each conversion returns 10-bit data left justified in a 16-bit unsigned result; the least significant 6 bits of each result equal zero. For mathematical simplicity each 2-byte result can be interpreted as a 16-bit unsigned number spanning the range 0x0000 to 0xFFFF (decimal 0 to 65,535). For example, converting a 2.5 Volt signal (representing half the 0 to 5V ATD input span) yields a result of 0x8000 (decimal 32768), equivalent to half of the full 16-bit numeric result range. Note that no bit-shifting is needed to use the conversion results. Another convenient side effect is that simply ignoring the least significant byte of a 2-byte conversion result yields a valid 8-bit result. This is explained below in the context of the ATDMultiple() routine.
| ATD Device Driver Routines Declared in the Analog.h file | ||
|---|---|---|
| ATD0_7_RESULTS | ATDMultiple() | ATDSample() |
| ATD8_15_RESULTS | ATDOff() | ATDSingle() |
| ATDDigitalInputs() | ATDOn() | ATDStartSample() |
Initializing the ATD converter
As explained in the Digital I/O chapter, the AN0-AN15 pins can be configured as either analog or digital inputs. Each pin has a digital I/O driver circuit that is controlled by a bit in the PORTAD0_MODE and PORTAD1_MODE registers (also called ATD0DIEN and ATD1DIEN, respectively). These and all of the 9S12/HCS12 register names are defined in the HCS12REGS.h file in the C:\MosaicPlus\c\libraries\include\mosaic directory. After a hardware reset, the AN0-AN15 pins are configured as analog inputs, with the digital I/O drivers and both 8-channel ATD converters off by default. See the entry for the ATDDigitalInputs() function in the C glossary for information on configuring some or all of these lines as digital inputs, and see the Digital I/O chapter of this document for information about reading digital data from these inputs.
If a pin on one of these ports is configured as a digital input, it is important that your system not present an analog input to that pin. An analog input driving a pin configured as a digital input can put the pin electronics in an intermediate logic state that results in high currents inside the processor chip.
To use one or more of the AN0-AN15 pins as an ATD input, its ATD converter must be turned on using the ATDOn() function. Given an input parameter channel number between 0 and 15, ATDOn() turns on the associated ATD converter and configures the pins as analog inputs by clearing all 8 bits in either PORTAD0_MODE (if the input parameter is between 0 and 7) or PORTAD1_MODE (if the input parameter is between 8 and 15). If the input channel_id is between 0 and 7, the ATD0_7_RESULTS converter is turned on and channels 0 through 7 are configured as analog inputs. If the input channel_id is between 8 and 15, the ATD8_15_RESULTS converter is turned on and channels 8 through 15 are configured as analog inputs. To turn on both converters (all 16 ATD channels) on the 9S12/HCS12 processor, execute:
ATDOn(0); ATDOn(8);
To configure some pins as analog inputs and some as digital inputs, first call ATDOn() for the specified set of 8 inputs, then call ATDDigitalInputs() with the appropriate bitmask. ATDOn() configures the specified converter system to return 10-bit left-justified results, and it puts the converter in the fast clear mode which relieves the program from the duty of clearing the flag bit that is set when the conversion is complete. If you explicitly write other values to the ATD configuration registers, the ATD control routines may not work properly.
The ATDOff() function accepts a channel number input parameter and turns the corresponding 8-channel ATD converter off. After the relevant ATD converter has been turned on, any of the conversion routines can be invoked. These include ATDSingle(), ATDSample(), ATDStartSample(), and ATDMultiple(). These are explained in detail below.
Performing a single conversion
The ATDSingle() function can be used to perform a single conversion on a specified channel in the range 0 to 15. This routine starts the conversion, waits for it to complete, and returns the result. The conversion uses the data format set by ATDOn() as 10-bit resolution, with the 10-bit data left justified in a 16-bit unsigned result; the least significant 6 bits of each result equal zero. For mathematical simplicity each result can be interpreted as a 16-bit unsigned number spanning the range 0x0000 to 0xFFFF (decimal 0 to 65,535). For example, converting a 1.25 Volt signal (representing one quarter of the 0 to 5V ATD input span) yields a result of 0x4000 (decimal 16384) which corresponds to one quarter of the full 16-bit numeric result range.
Converting 1 to 8 channels in sequence
The ATDSample() routine converts up to 8 channels in sequence, and returns a 16-bit pointer to the result register frame in common memory. Its function prototype is:
uint* ATDSample ( int starting_channel_id, int numchannels )
The starting_channel_id (an integer in the range 0 to 15) and numchannels (an integer in the range 1 to 8) parameters specify a sequence of up to 8 channels converted in order with rollover modulus 8. Note that channels 0 to 7 are on the ATD0_7_RESULTS converter, and channels 8 to 15 are on the ATD8_15_RESULTS converter, so the channel after 7 in a sequence is 0, not 8. Similarly, the channel after 15 is 8. Once started, the ATD automatically converts each of the channels in the sequence (up to the specified numchannels in the range 1 to 8) one time at 7 microseconds (μs) per conversion. In other words, the conversion time between channels within a sequence is always 7 μs. The total execution time of this routine is approximately:
(7μs * numsamples) + 3.5 μs
Before starting a new conversion, results should be fetched out of the returned result register frame which starts at either the 16-bit address ATD0_7_RESULTS or ATD8_15_RESULTS; the relevant 16-bit address is returned by this routine. This result register frame contains eight 16-bit result registers. The first result in the sequence (corresponding to starting_channel) is at byte offset 0, the next at offset 2 bytes, then offset 4 bytes, etc., for the specified numchannels. Make sure you take account of C’s pointer arithmetic when fetching data, as the return type is declared as a pointer to an unsigned 16-bit integer. The C pointer arithmetic will automatically increment the pointer by 2 bytes in response to a ++ operation. The conversion returns the data as 10-bit resolution, left justified unsigned results with the least significant 6 bits of each result equal to zero. For mathematical simplicity each left-justified result can be interpreted as a 16-bit result spanning the range 0x0000 to 0xFFFF (decimal 0 to 65,535). For example, if the starting channel is 4 and numchannels equals 8, then samples are stored in the result registers in the following order:
4 5 6 7 0 1 2 3
The ATDStartSample() routine is similar to ATDSample(). Given starting_channel_id and numchannels parameters, it starts the conversion of a single sequence of up to 8 ATD channels. Unlike ATDSample(), ATDStartSample() exits without waiting for the conversion(s) to complete, and does not return a pointer to the result register frame. ATDStartSample() is useful in customer-coded interrupt service routines: you can read the prior conversion results from the result registers, then start the next conversion without waiting for results. This makes for fast operation, as the conversions take place between the interrupt services at the rate of 7 microseconds (μs) per channel. Prior results should be fetched out of the appropriate result register set, starting at either ATD0_7_RESULTS or ATD8_15_RESULTS; each of these constants is the base address of eight 16-bit result registers.
Converting multiple sequences with timing control
ATDMultiple() is the most capable and feature-rich ATD control function. Its function prototype is:
void ATDMultiple ( xaddr buffer, uint utime, int one_byte, int numsequences, int starting_channel_id, int numchannels );
This routine converts multiple sequences comprising the specified numchannels per sequence, and stores the conversion results as 8- or 16-bit values into a memory buffer starting at the specified 32-bit buffer xaddress. If the one_byte flag is true, each sample occupies 1 byte in the buffer, and this constrains the results to 8-bit resolution per sample, with each sample result in the range 0 to 255. If the one_byte flag is false, each sample occupies 2 bytes in the buffer, and each sample has 10-bit resolution, with the 10-bit data left justified in a 16-bit unsigned result, and the least significant 6 bits of each result equal zero. For mathematical simplicity each 2-byte result can be interpreted as a 16-bit unsigned number spanning the range 0x0000 to 0xFFFF (decimal 0 to 65,535). For example, converting a 2.5 Volt signal (representing half the 0 to 5V ATD input span) yields a 2-byte result of 0x8000 (decimal 32768) if the one_byte flag is false, or an equivalent 1-byte result of 0x80 (decimal 128) if the one_byte flag is true.
If the one_byte flag is true, the specified results buffer must be at least one byte larger than the number of samples; that is:
buffer_size = (numsequences * numchannels) + 1 // if one_byte flag is true
This is because ATDMultiple() actually stores 2 bytes per sample, and, if the one_byte flag is true, overwrites the least significant byte of the prior sample with the next sample’s most significant byte. This works because each 10-bit data field is left justified in the 16-bit result field, so overwriting the least significant byte (in higher memory) leaves the most significant 8 bits of the result intact. If the one_byte flag is false, the required buffer size is:
buffer_size = 2 * (numsequences * numchannels) // if one_byte flag is false
This routine performs multiple analog-to-digital conversions with the unsigned integer utime input parameter specifying a programmable inter-sequence sampling time with 2.5 microseconds (μs) quantization as explained below. The starting_channel_id parameter in the range 0 to 15, and the numchannels parameter in the range 1 to 8, together specify a sequence of up to 8 channels converted in order with modulus 8 rollover. As explained above, channels 0 to 7 are on the ATD0_7_RESULTS converter, and channels 8 to 15 are on the ATD8_15_RESULTS converter, so the channel after 7 in a sequence is 0, not 8. Similarly, the channel after 15 is 8. Once started, the ATD automatically converts each of the channels in the sequence (up to the specified numchannels in the range 1 to 8) one time at 7 μs per conversion. In other words, the conversion time between channels within a sequence is always 7 microseconds. The numsequences parameter is an unsigned integer that specifies the number of such sequence conversions that are performed. The conversion results are stored starting at the specified 32-bit buffer xaddr. After all the conversions within a sequence have been performed, there is an additional inter-sequence delay of
inter-sequence_delay = (2.5μs * utime) + overhead_delay
where the overhead_delay averages 3 μs if xaddr is in common RAM, or 6.5 μs if xaddr is in paged RAM. Inter-sequence timing jitter (that is, the variation in overhead_delay from sequence to sequence) is less than 0.2 μs, and there is no jitter within a sequence. If a page crossing occurs between sequences, add 1 μs of overhead_delay and an additional 0.2 μs of potential jitter to the inter-sequence time. The user-specified utime parameter is an unsigned integer which is multiplied by 2.5 μs and added to the overhead_delay after each sequence to specify the conversion timing.
ATDMultiple() timing analysis
The ATDMultiple() routine uses a software timing delay to set the inter-sequence timing interval. The following timing analysis is accurate for a single-task application with no interrupts running. Multitasking or interrupt service routines will increase the sampling intervals. The simplest timing case involves calling this routine with 1 channel per sequence (numchannels = 1), in which case the inter-sample time depends on whether the xaddr buffer is in common RAM or paged RAM, as follows:
sampling_period = 7μs + (2.5μs * utime) + 3 μs // if xaddr is in common RAM sampling_period = 7μs + (2.5μs * utime) + 6.5 μs // if xaddr is in paged RAM
In the first case, with utime = 0, sampling occurs every 10μs = 100KHz sampling. In the second case, with utime = 0, sampling occurs every 13.5μs = 74 KHz sampling. Increasing the utime parameter increases the inter-sequence sample time and decreases the sampling frequency. For example, with numchannels = 1 (1 channel per sequence), utime = decimal 96, and the buffer xaddress in common RAM, the inter-sample time is:
7μs + (2.5μs * 96) + 3μs = 250 μs
which corresponds to a sampling frequency of 4 KHz. If there is more than 1 channel per sequence, then the sampling process can be thought of as a burst of samples within the sequence separated by 7 μs per sample, followed by an inter-sequence delay. For example, assume that the starting channel is 4, numchannels = 8, utime = 0, and the storage buffer xaddress is in paged memory. In this case, the samples are stored in memory in the following order:
4 5 6 7 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 1 2 3 ...
Each sample within the sequence takes 7μs, and the inter-sequence delay is:
inter-sequence_delay = 0 * 2.5uμs + 6.5μs = 6.5μs.
Thus the total time between samples of a given channel equals
sampling_period = numsamples * 7μs + 6.5μs = 56 μs + 6.5μs = 62.5 μs,
corresponding to a 16KHz sampling rate for each channel. If we modify this example by changing utime to decimal 15, then the total time between samples of a given channel equals:
sampling_period = 8 * 7μs + (2.5μs * 15) + 6.5μs = 56μs + 37.5μs + 6.5μs = 100 μs
This corresponds to a 10KHz sampling rate for each channel.
Fundamentals of analog to digital conversion
An analog to digital converter samples an analog signal and outputs a digital number that is proportional to the analog signal. The two 8-channel ATD converters on the PDQ Board sample input voltages and communicate the digital results to the 9S12/HCS12 processor.
The analog input signal must be within the input range of the ATD converter. On the PDQ Board, the lower bound of the range is equal to the analog ground (AGND) voltage on VRL (voltage reference/low) and the upper bound of the allowable input range is equal to the +5VAN analog voltage supply on VRH (voltage reference/high). By default, their values are 0 Volts (analog ground) and 5.0 Volts (+5VAN), respectively. Thus the nominal full-scale range of the ATD converter on the PDQ Board is 5 Volts. AGND and +5VAN are accessible at the Analog I/O Field Header on the PDQ Board.
The converter measures the input voltage with a specified resolution. The resolution is the granularity with which the measurement is performed. It can be specified as a number of bits or as a voltage increment. For example, an ATD converter with only 1 bit of resolution and a 5 Volt input range would classify all voltages from 0 to just under 2.5 Volts as the digital value 0, and voltages from 2.5 Volts to 5 Volts as the digital value 1. This converter would have a resolution equal to 1 bit, corresponding to 2.5 Volts per count.
An ATD converter measures the input voltage with a specified accuracy. The accuracy tells how close the measured value is to the actual voltage. A typical 10 bit ATD converter is accurate to within plus or minus one least significant bit, equivalent to plus or minus 1/1024 of the input range.
The converter on the PDQ Board returns the result as a 10-bit field left-justified in a 16-bit value, with the least significant (right-most) 6 bits set to 0. The following sections describe how to calculate the resolution of a converter, and how to convert a result to its equivalent voltage. In this case, the resolution of the result (10 bits) is not the same as the field size of the result (16 bits). It is important to distinguish between resolution and field size, as the following discussion makes clear.
Determining the resolution of an ATD converter
The VRL and VRH analog input reference pins define the lower and upper voltages that can be converted by the 10 bit ATD. The resolution depends on the input voltage range. The measurement resolution of an n-bit ATD, expressed in Volts per least significant bit (LSB), is
Resolution = (VRH - VRL) / 2n [Volts per LSB]
where 2n is the number of counts that can be represented by an n-bit number. From this equation we see that resolution becomes finer (better) as B grows larger or as the reference voltage range (VRH - VRL) gets smaller. For the 10 bit ATD the resolution is
10 bit Resolution = (VRH - VRL)/1024 [Volts per LSB]
With the default VRL and VRH of 0 V and +5 V, respectively, the resolution of the 10 bit converter on the PDQ Board is 4.88 mV per least significant bit. If only one byte (the most significant byte of the 16-bit conversion result) is kept (as when a true one_byte flag is passed to the ATDMultiple() function), then the converter behaves as an 8-bit ATD. The resolution of an 8 bit conversion on the PDQ Board is 19.5mV per least significant bit.
Converting the 9S12 ATD result into its equivalent analog voltage
The ATD on the 9S12/HCS12 MCU is a unipolar converter that converts a positive voltage into an unsigned positive integer result. It converts voltages ranging from 0 to 5V into a 10-bit number left justified in a 16-bit field, ranging from 0 to 0xFFC0 as a hex number (r 65472 decimal). Assuming that the VRL (low ATD reference voltage) equals 0, then if we take the ratio of the returned conversion value to its full scale value, the result should be equal to the ratio of the measured voltage to the full scale reference voltage. This common sense reasoning allows us to calculate the equivalence between a conversion result and the corresponding input voltage.
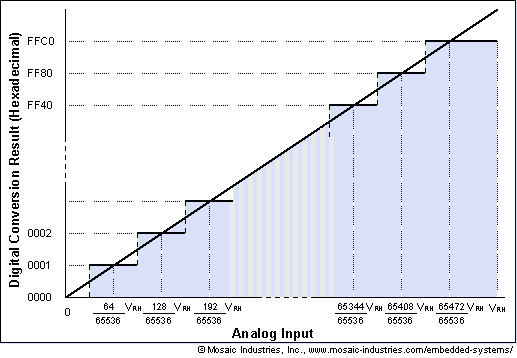
As explained earlier in this chapter, the default ATD conversion results ore formatted as 10-bit data left justified in a 16-bit field. The full scale numeric value of a 16-bit number is 216, or 65,536 counts. This is the numeric denominator of our ratio; the numerator is the returned 16-bit result. Because the least significant 6 bits of the result equal 0, note that each incremental count adds 26 = 64 counts to the numerator. Figure 2 illustrates the conversion result versus analog input for a 10-bit ATD that returns its result in a 16-bit field.
On the voltage side of our ratiometric equation, the full-scale voltage equals VRH - VRL which is nominally 5 Volts. Thus, to convert the 16-bit result (10 bits left justified in a 16-bit field) returned by the ATD converter into an equivalent voltage, use the formula:
16-bit_Conversion_result / (216) = Input_voltage / (VRH - VRL)
Rearranging this equation to isolate the Input_Voltage yields:
Input_Voltage = [16-bit_Conversion_result * (VRH - VRL)] / (216)
Substituting the nominal 5 Volt value for VRH - VRL and noting that 216 = 65,536, we find that the nominal calculated input voltage is:
Input_Voltage = [16-bit_Conversion_result * (5V)] / (65,536)
This equation is valid for results that are returned by the 9S12/HCS12 converters as 16-bit values, assuming that the VRL (low ATD reference voltage) equals 0. If VRL is non-zero, the offset between VRL and the desired absolute ground reference should be added to the right hand side of Eqn. 11-5.
If only one ATD result byte (the most significant byte of the 16-bit conversion result) is kept (as when a true one_byte flag is passed to the ATDMultiple() function), then the converter behaves as an 8-bit ATD. In this case the full-scale numeric value is 2<sup8</sup> = 256, and the Input_Voltage can be expressed as:
Input_Voltage = [8-bit_Conversion_result * (5V)] / (256)
If VRL is non-zero, the offset between VRL and the desired absolute ground reference should be added to the right hand side of the equation.
Using the 9S12/HCS12 ATD converter
The following sections describe the C language software routines used to control the ATD subsystem of the HC12/9S12/HCS12 MCU used on the PDQ Board.
Examining the demonstration program
The code discussed in this section is located in the "Analog I/O Demo" project.
Some of the functions in this file are interactive versions of functions described above and declared in the C:\MosaicPlus\c\libraries\include\mosaic\ANALOG.H file. These functions are also described in detail in the C Glossary.
We recommend that you compile and download the "Analog I/O Demo" project now so that you can interactively work through the exercises in this chapter. After opening the project, simply click Build→ Build. Then enter the Mosaic Terminal program, and type:
COLD↓
to terminate any prior multitasking program that might be running, and select the Send File menu item to send PDQ_ANALOGIO.DLF to the PDQ Board.
Initializing the ATD
Two 8-channel 10-bit ATD systems reside in the 9S12/HCS12 processor chip. The 16 analog inputs are accessed via pins AN0 through AN15 on the PDQ Board’s Analog I/O Field Header. These lines can be configured as analog or digital inputs as explained above. To configure all 16 lines as analog inputs, execute the following code:
ATDOn(0); // turn on converter for AN0-AN7 ATDOn(8); // turn on converter for AN8-AN15
In the PDQ_ANALOGIO.c file, these ATDOn() statements are included in the InitAnalog() function, which also initializes the buffers used by ATDMultiple() as explained below. In an autostarting application that uses analog inputs, you should include the appropriate ATDOn() statement(s) in code called by main().
ADC hardware connections
To sample an analog voltage, attach a voltage with a value between zero and +5 Volts to one of the analog input channels. For example, to sample channel 0, connect the analog voltage to pin AN0 at pin 24 of the Analog I/O Field Header. To sample channel 15, connect a voltage to pin AN15 at pin 9 of the Analog I/O Field Header.
Each analog signal is converted to a 16-bit number indicating its value relative to VRL (the low voltage reference) and VRH (the high voltage reference). The default values are VRL = 0 Volts (AGND) and VRH = 5 Volts (+5VAN). The AGND and +5VAN signals that drive VRL and VRH are brought out to pins 1 and 2 of the Analog I/O Field Header. The exact voltage difference between analog ground and analog +5V varies slightly from board to board; it is a good idea to measure this voltage difference on your board to obtain the most exact voltage equivalents of the measured ATD results using Eqn. 11 4 above.
Interactively perform the A/D conversions
Before we make any conversions the ATDOn() function needs to execute. Since this function executed with main, simply type:
main↓
The Convert10() function is defined near the top of the PDQ_ANALOGIO.c file. You can see from its definition that it is simply an interactively callable version of the ATDSingle() function. Now that you have connected an input voltage to channel AN0, you can type from your terminal:
Convert10( int 0)↓
The printed return value summary displays the conversion count; you’ll see a printout that looks something like this for a 1.5 volt signal:
Rtn: -30722 19648 =0x87FE4CC0 =fp: -3.822E-34
We know that this function returns an integer, so we identify 19648 (hex 0x4CC0) as the return value; the other numbers in the summary are irrelevant. If the input is 1.5 volts with the known full scale 5 volt range, the result should be:
(1.5 / 5.0) * 65,536 = 19,648 = 0x4CC0
If the input voltage equals VRL (the low reference voltage, typically at 0 Volts), the result will equal 0. If the input is within 1 bit of VRH (the high reference voltage, typically at 5.0 Volts), the result will equal hexadecimal 0xFFC0; this number has all but the least significant 6 bits equal to 1, and corresponds to decimal 65,472. You can see these values graphically illustrated in Figure 11-1 .If the input is exactly half of (VRH - VRL), the result will equal decimal 32,768 (hex 0x8000).
Multiple ADC conversions with results stored in a C array
The SampleToForthArray() function defined in PDQ_ANALOGIO.c invokes the ATDMultiple() function which is described in detail above. SampleToForthArray() repeatedly converts a specified channel for numsamples times with a delay of 4095 microseconds per sample, and stores the results as single bytes in a one-dimensional forth array named forth_results_8. At the maximum sampling speed it can sample up to 100 kHz.
Because we have connected the channel 0 input (AN0), let’s perform multiple conversion on this channel. Type at your terminal:
SampleToForthArray( int 0)↓
remembering to type at least one space after the ( character. This function does not return a value, so the printed return value summary is not relevant. We have setup a special variable called forth_base which points to the address of the first sample. You can use the debugging routine named DUMP to view a hexadecimal dump of the buffer we just sampled to. Type at your terminal:
forth_base 2@ F DUMP↓
DUMP is a QED-Forth function that expects as inputs an address and a number of bytes to dump. In this case, forth_base puts a pointer address on the data stack, 2@ dereferences the pointer and returns a 2 byte address, and F is the number of bytes to be dumped (15). You should see a printout similar to this if you connected a 1.5 volt signal:
pg addr 04 05 06 07 08 09 0A 0B 0C 0D 0E 0F 00 01 02 03 456789ABCDEF0123 18 8004 4D 4D 4D 4D 4D 4D 4D 4D 4D 4D 4D 4D 4C 4D 4D 4D MMMMMMMMMMMMLMMM
This tells us that the contents of the 16 bytes starting at address 0x8004 (which is the address of forth_base) all equal 0x4D. To the right of the hex dump the ascii equivalent of the memory contents is displayed; this is not relevant for the numerical data here. We conclude that the ATD conversion result was 0x4D, equivalent to decimal 77. We can back-calculate the equivalent voltage as:
(77 / 256) * 5V = 1.5V
as expected. Your results may vary depending on the voltage you present to AN0 and the exact value of the +5VAN supply voltage on the PDQ Board.
Analog reference voltage
The A/D converter converts input signals between two reference voltages that are applied to special pins of the processor chip: a negative reference voltage (nominally ground), which represents the zero level; and a positive reference voltage (nominally 5 V), which represents the full scale voltage which is converted to the full scale 10-bit number left justified in a 16-bit field (0xFFC0 as a hex number, or 65472 decimal).
The internal A/D converter's negative reference voltage is connected to the board's digital ground at only a single point – at pin 1 of the Analog header H4, labled AGND. You should use that pin for the signal return of any signals applied to the analog inputs for conversion. For example, if you use an analog isolator to overcome ground loop problems, the signal return output of the analog isolator should be connected directly to pin 1 of H4, and not to circuit ground anywhere else. Likewise, the output reference voltage pin of a differential amplifier should be connected directly to pin 1 (AGND), rather than to the board's digital ground. See the page on Precision Measurement Without Ground Offsets for more guidance.
When filtering analog signals before applying them to the A/D input pins, return the capacitors of the filters to AGND pin 1.
The AGND of pin 1 is connected to the PDQ Board's digital ground on the board near pin 1 by a zero ohm resistor, R44. If needed, that connection can be broken by removing R44. That would be useful if you need to compress the A/D converter's range, for example for converting voltages ranging from 2V to 5V instead of 0V to 5V.
The positive reference voltage for the processor's internal A/D, +5VAN, is derived onboard from the +5V digital power rail by conditioning with an RLC low-pass filter (with a low-pass cutoff frequency of 4 kHz and a resistance of 1.5 Ω) that prevents digital noise from being applied to the A/D reference voltage. The +5VAN reference is also brought out to the analog header, H4, at pin 2.
If you use ratiometric sensors that require a full scale reference voltage, you can use +5VAN for that.
Because the internal resistance of the reference supply is about 1.5 Ω, drawing current will cause the voltage to drop slightly below the +5V digital supply. To prevent overheating of onboard components, do not draw more than 30 mA from the +5VAN pin.
Source impedance considerations
When you make electrical connection to the A/D input pins you must take into account the impedance of the source of the voltage you are measuring and its influence on the conversion accuracy. More specifically, three attributes of the source will determine the accuracy of the measurement: its resistance, its capacitance and that of any filter capacitors you provide, and any overload current the source may inject into an A/D pin.
Source resistance
The source resistance can cause two components of offset voltage, one static, and one related to the sampling frequency:
- Static offset error – Like all the 9S12's input pins, the A/D input pins draw a small static leakage current, of up to ±1μA over the entire temperature range. That current introduces an offset voltage as it flows through the source resistance. The maximum source resistance allowed to preserve the full accuracy of the A/D over its entire temperature range is approximately 1 KΩ. That causes a 1mV offset error, corresponding to 1/5 of a LSB. A 2.5 KΩ source resistance would cause a worst case ±1/2 LSB error. If operating conditions are near room temperature or leakage-induced error is acceptable, larger values of source resistance may be allowed.
- Dynamic offset error – Another current is caused by the dynamic sampling of the input pin by the A/D. Each time the pin is sampled, an internal 12pF capacitor charges and discharges. That produces a small, frequency dependent current which, like the static current, flows through the source resistance. The magnitude of that current is approximately given by I=fCV, where V=5V, C=12pF, and f is the sample frequency. Its magnitude is appx. 0.6 μA/10kHz, or 0.6μA of current for each 10kHz of sampling frequency. Consequently, if you sample at 17kHz and have a source resistance of 1 KΩ you can expect an offset of 1mV, or about 1/5 of a LSB.
Source capacitance
When sampling, the A/D switches its 12pF internal capacitor to the input. That causes a small voltage drop due to charge sharing with the external and pin capacitances. If there is an external capacitance isolated from the source by an appreciable source impedance, than its voltage will drop slightly as the sampling capacitance is switched to it. For a maximum sampling error of the input voltage ≤ 1 LSB, then any external filter capacitor should be large enough, as,
Current injection
You should not allow an A/D input pin to be driven below ground or higher than the supply voltage. If that happens internal substrate diodes within the processor will start conducting, and unless the current is limited the device could be destroyed.
If the input current resulting from an over- or under-voltage condition is limited to less than ± 2.5mA the device will continue to work, and if conversions are done on the input channel the results will saturate at either the upper (0xFFC0) or lower (0x0000) extreme. If an adjacent channel is sampled, its results may be distorted slightly, as some of the overload current seeps into its input and flows through the source resistance. The amount that seeps into an adjacent channel is 10-4 of the overload current for an overvoltage condition, and 10-2 of the overload current for an undervoltage condtion. A channel will be affected by the sum of the overload currents into each of its neighboring channels, with the appropriate portion of that overload current flowing through its source resistance.
If the overload current is greater than ± 2.5mA all bets are off! That exceeds the single pin limit for the processor, and the processor may be damaged.
See also → Serial Communications

