Pulse Width Modulated I/O
What is pulse width modulation (PWM)?
The timer/counter channels of the Freescale 9S12/HCS12 microcontroller excel at generating PWM signals. A pulse-width-modulated (PWM) signal is a periodic digital output waveform with a controlled period, duty cycle, and polarity. These waveforms can be used to drive stepper motors, servo-motors, AC and DC relays, LEDs (Light-Emitting Diodes), and many other actuators that are useful in instrument control applications. By varying the duty cycle (the percentage of the time that the PWM output is in its active state), the average value of the PWM signal can be changed. That's very useful; PWM can be employed to vary the intensity of light put out by an LED, or the speed of a motor, for example. A PWM signal can be smoothed with a low-pass filter to create an analog output whose value is proportional to its duty cycle; this provides a way of creating a simple D-to-A (Digital-to-Analog) converter. The PWM modulator may also be used as a frequency generator or pulse generator.
The operating system includes precoded software driver functions to control the PWM system. By simply passing the PWM channel identifier to these functions, you can configure the period, duty cycle, active state, alignment, resolution, and clock source of each PWM output. This chapter describes the architecture of the HCS12’s PWM system, and discusses how to use the driver functions.
The PDQ Single Board Computer (SBC) incorporates a Freescale 9S12 (HCS12) processor that provides eight independent channels of PWM output. Once set up the channels run autonomously, without the need for software intervention. Each of the eight channels has a programmable period and duty cycle as well as a dedicated counter. A flexible clock select scheme allows a total of four different clock sources to be used with the counters. Each of the modulators can create independent continuous waveforms with software-selectable duty cycles from 0% to 100%. The PWM outputs can be programmed as left aligned outputs or center aligned outputs. Briefly, the PWM channels include these distinctive features:
- Eight independent PWM channels with programmable period and duty cycle.
- Dedicated counter for each PWM channel.
- Programmable PWM enable/disable for each channel.
- Software selection of PWM duty pulse polarity for each channel.
- Period and duty cycle are double buffered. Change takes effect when the end of the effective period is reached (PWM counter reaches zero) or when the channel is disabled.
- Programmable center- or left-aligned outputs on individual channels.
- Eight 8-bit channel or four 16-bit channel PWM resolution.
- Four clock sources (A, B, SA and SB) provide for a wide range of frequencies.
- Programmable Clock Select Logic.
- Emergency shutdown.
Unfortunately, the Freescale documentation's use of the word duty is a little confusing. They often use it to refer to duty cycle but also to the number of ON counts of the PWM output register. When referring to a parameter passed to a function to set the ON counts of the PWM register we will follow Freescale's convention and use the term duty. In all other cases we will use the term duty cycle to refer to the percentage ON time, or ratio of ON time to period.
That is,
Period = CP = CON + COFF
Duty cycle = CON/CP = CON/(CON + COFF)
The architecture of the HCS12 PWM hardware module
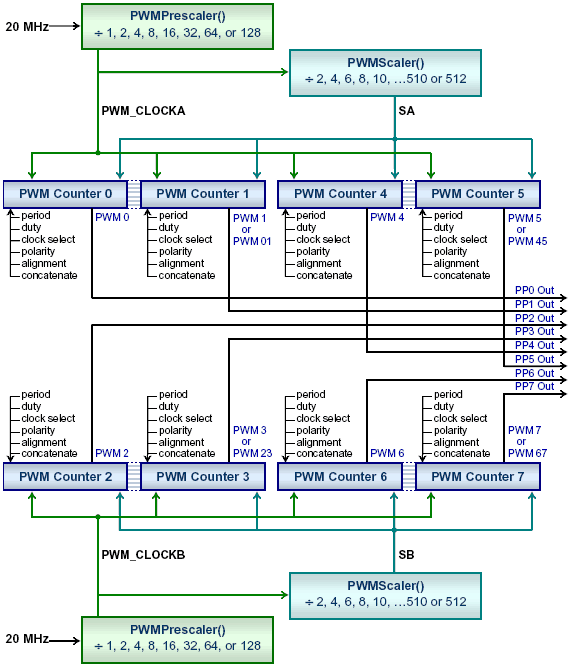
The PWM (pulse width modulation) subsystem in the HCS12 processor provides eight 8-bit or four 16-bit PWM outputs on PORTP. The PWM signals are generated without the need to interrupt the processor. This results in accurately timed waveforms without burdening the processor. These output lines are named PP0 through PP7 on the Digital I/O Field Header of the PDQ Board.
The operation of the PWM subsystem is illustrated by the following diagram:
Channel attributes are summarized in the following table:
| Channel | PWM Clocks | PWM Resolution | |
|---|---|---|---|
| PP0 | PWM_CLOCKA / SA | – | 8-bit or none |
| PP1 | PWM_CLOCKA / SA | – | 8- or 16-bit |
| PP2 | – | PWM_CLOCKB / SB | 8-bit or none |
| PP3 | – | PWM_CLOCKB / SB | 8- or 16-bit |
| PP4 | PWM_CLOCKA / SA | – | 8-bit or none |
| PP5 | PWM_CLOCKA / SA | – | 8- or 16-bit |
| PP6 | – | PWM_CLOCKB / SB | 8-bit or none |
| PP7 | – | PWM_CLOCKB / SB | 8- or 16-bit |
Briefly, each PWM channel is controlled by a PWM counter. In operation, the counter is continuously incremented by clock pulses, from a count of zero to a count of period-1, after which it rolls over to zero again. For the first duty clock pulses the output is set active (i.e., ON), then it is set to inactive (i.e., OFF) for the remainder of its period.
A set of HCS12 control registers configures each PWM output on PORTP. You can set the period of the counter and its active time (duty) in clock ticks, and you can choose its clock frequency from a prescaled clock or a prescaled and scaled clock. You can change the prescaling and scaling factors for goups of four channels at a time. You can also choose whether the active state of each output is a logic low or high, and whether the active state is centered or left-aligned with in the output waveform. The following sections describe these options in detail.
Reading the current state of the PWM output
If one or more PORTP pins are configured as PWM outputs, the specified pin will become an output regardless of the value written to the PORTP_DIRECTION (also called the DDRP) register. In this case, the PWM system will control the pin levels regardless of the data written into the PORTP register. Consequently, to read back the state of PORTP when there are active PWM-controlled pins, the PORTP_IN register should be read instead of the PORTP register. This is because PORTP_IN returns the actual logic levels on the pins, while PORTP reads back the last value written to the PORT register.
PWM resolution
The eight PWM channels may be used to produce eight independent, 8-bit resolution outputs, or pairs of channels may be combined to make four, 16-bit resolution outputs.
Using 8 bit resolution
The default resolution of the eight PORTP PWM outputs is 8 bits, meaning that the period and on time can be specified with a resolution of 1 part in 255. Each 8-bit PWM output is referred to by its bit number on PORTP; valid 8-bit PWM identifiers are in the range 0 through 7.
| Using 8-bit resolution | |
|---|---|
| Channel Identifier | Output Pin |
| 0 | PP0 |
| 1 | PP1 |
| 2 | PP2 |
| 3 | PP3 |
| 4 | PP4 |
| 5 | PP5 |
| 6 | PP6 |
| 7 | PP7 |
Most of the functions that control a PWM channel, for example PWMEnable and PWMSetup, expect the channel identifier as an input parameter – you can use the simple integers 0 through 7.
Using 16-bit resolution
Pairs of channels can be concatenated to form a 16-bit PWM output with resolution of 1 part in 65,535. Each 16-bit PWM output is referred to by one of the identifiers PWM01, PWM23, PWM45, or PWM67 as defined in the C:\MosaicPlus\c\libraries\include\mosaic\PWM.h file. The numerically higher channel in a concatenated pair supplies the output pin. For example, the PWM01 16-bit output appears on pin PP1 (pin 1 of PORTP).
| Using 16-bit resolution | |
|---|---|
| Channel Identifier | Output Pin |
| PWM01 | PP1 |
| PWM23 | PP3 |
| PWM45 | PP5 |
| PWM67 | PP7 |
Most of the functions that control a PWM channel, for example PWMEnable and PWMSetup, expect the channel identifier as an input parameter – you can use the identifiers PWM01, PWM23, PWM45 or PWM67.
When you are using 16-bit resolution PWM, the PWM signal is produced on the output pin corresponding to higher channel of the pair of counters used; no signal is produced on the pin corresponding to the other counter of the pair.
Active high or active low
Each signal can be configured as either active high or active low. An active high PWM signal starts each period in the high state and stays high until the counter equals the contents of the duty register, at which time it goes low. An active low PWM signal starts each period in the low state and stays low until the PWM counter register equals the contents of the duty register, at which time the output goes high.
Center aligned waveforms
In certain applications, it is convenient to center-align each PWM period such that the signal is symmetric about the mid-point of the period. The PWM system on the HCS12 lets you configure each PWM output as a standard left-aligned, or a center-aligned signal. For left aligned outputs, the PWM counter starts at 0 and counts up to the value stored in the PWM period register, and then resets to zero to start the next cycle; the period equals the value in the period register. For center aligned outputs, the counter starts at 0 and counts up to the value stored in the period register(s), and then counts down to zero. Consequently, the output period of a center-aligned signal is twice the value stored in the period register(s).
For left-aligned PWM outputs, the duty register specifies the number of counts in the active state. For center-aligned PWM outputs, the number of counts in the active state is twice the value in the duty register. Because the period is also doubled, the percentage duty cycle in the active state is still equal to the duty register contents divided by the period register contents. The center-aligned output starts out and stays active until the counter equals the contents of the duty register, at which time it toggles to the inactive state. For center-aligned outputs, the counter counts up to the period then counts down, so the output toggles inactive during the up half-cycle, and re-toggles to the active state during the down half-cycle.
Clocking the PWM counters
The PWM system provides four clock sources that can be used to increment the PWM counter registers. Two of the clock sources apply to one set of four channels, while the other two apply to the other set of four channels. The eventual frequency of the PWM output depends on the clock frequency and the number of clock counts in the PWM period. You can change the frequency of a channel in several ways:
- You can choose between the two clock sources;
- You can alter the frequency division factor for each of the clock sources;
- You can change the number of clock counts in the period of the PWM waveform.
The two main clock sources are named PWM_CLOCKA, which may be used for channels 0, 1, 4, and 5, and PWM_CLOCKB, which may be used for channels 2, 3, 6, and 7, as defined in the C:\MosaicPlus\c\libraries\include\mosaic\PWM.h file. These clocks are derived from the 20MHz system clock by dividing it by a prescale factor. The period of PWM_CLOCKA and PWM_CLOCKB can be software selected to be 1, 2, 4, 8, 16, 32, 64, or 128 times the 50 nanosecond ( 20 MHz ) bus clock (E-clock) period using the PWMPrescaler() routine. The frequencies of PWM_CLOCKA and PWM_CLOCKB are then given as,
where,
the prescale factors, FPSA and FPSB, can be chosen as powers of two (1, 2, 4, 8, 16, 32, 64, or 128).
The 20MHz frequency is reduced (the period is increased) by the prescale factor. Using PWM_CLOCKA and PWM_CLOCKB you can have clock frequencies from 20MHz to 156.25 kHz.
These clocks may be further frequency divided to provide scaled versions of each. These are called SA and SB. No C-callable constants are defined for the scaled clocks; rather, you specify that they are to be used by calling the PWMScaledClock() function.
The frequencies of the scaled clocks, SA or SB, are set by a scale factor sent to the PWMScaler() function. Those scale factors can be any even integer from 2 to 512. The frequencies of SA and SB are then given as,
where,
the prescale factors, FPSA and FPSB, can be chosen as powers of two (1, 2, 4, 8, 16, 32, 64, or 128), and,
the scale factors, FSA and FSB, can be chosen as even integers from 2 to 512 (2, 4, 6, 8, … 510, or 512).
These scaled clocks further reduce the frequency of the PWM_CLOCKA or PWM_CLOCKB by the scale factors you choose, with rather fine resolution. You can then have clock frequencies down to 305 Hz, and PWM frequencies down to 1.2 Hz.
The 8-bit PWM channels 0, 1, 4, 5, and 16-bit channels PWM01 and PWM45 can be clocked from either the prescaled PWM_CLOCKA or the prescaled and scaled SA. The 8-bit PWM channels 2, 3, 6, 7, and 16-bit channels PWM23 and PWM67 can be clocked from either PWM_CLOCKB or SB.
PWM ON time, period and duty cycle
The PWM period register specifies the number of clock counts in the PWM period (although center-aligned signals have twice the register period as described below). The PWM counter register keeps track of the progress of the PWM signal within a single period. The PWM duty register sets the number of ON clock counts. The duty cycle is then the ratio of ON time to the total period, or the fractional time relative to the period that the signal is in its active state.
For standard left aligned outputs, the PWM counter starts at 0 and counts up to the value stored in period - 1, and then resets to zero to start the next cycle; as a result, the period of the signal produced equals the value in the period register for standard left aligned signals. For center aligned outputs, the counter starts at 0 and counts up to the value stored in the period register, and then counts down to zero. This symmetrical up/down counting approach ensures a center aligned signal, and it also results in an output period that is twice the value stored in the period register. In each case, when the counter value matches the duty value, the output changes state.
For standard left-aligned outputs, the PWM frequency is given by its clock frequency divided by the number of counts in its period,
fPWM = fc / CP
For example, if the prescaled and scaled version of the clock, SA, is used, the frequency is given by,
fPWM = f0 / (FPSA FSA CP)
For center-aligned outputs, the period is doubled as described above,
fPWM = f0 / (2 FPSA FSA CP)
The PWM signal's period, in seconds, is the inverse of its frequency, as,
Period = 1/fPWM
When we set up each channel we send it a duty parameter as the number of clock counts for the output's active or ON state (whether we set it up for active low or active high), and a period as the total number of clock counts in the cycle. The duty cycle, or percentage ON time, is then,
DPWM = [Duty_contents / Period_contents] = CON/CP
In the above equations, the Period_contents represents the 8- or 16-bit contents of the PWM period register (for 8- or 16-bit PWM channels, respectively). The Duty_contents represents the 8- or 16-bit contents of the PWM duty register. For 16-bit PWM channels, the counter, duty and period registers are 16-bit concatenations of the registers of the two component 8-bit PWM channels.
PWM update timing
Updates to the period or duty registers typically take effect at the next period boundary. This helps to minimize unwanted transients in the waveform. Writes to the PWM counter register reset the count to zero, and start a new PWM period. If the contents of the PWM period register equal 0, or if the duty register contents are greater than or equal to the period register contents, then the PWM output is a static unchanging signal in its active state (active high or active low, as set by the driver functions explained below).
The PWM software drivers
A suite of software drivers for the PWM system is included in the operating system on the PDQ Board. The following table summarizes these functions and macros; consult the C Glossary for detailed definitions. These routines implement all of the features of the PWM system with the exception of the "emergency shutdown" feature which is explained in the Freescale PWM documentation. After presenting an overview of the driver routines, some coded examples will be presented to illustrate their use.
| PWM Driver Routines as Declared in the PWM.h file. | ||
|---|---|---|
| PWM01 | PWMConcatenate() | PWMLeftAlign() |
| PWM23 | PWMCounterRead() | PWMPeriodRead() |
| PWM45 | PWMCounterWrite() | PWMPeriodWrite() |
| PWM67 | PWMDisable() | PWMPrescaler() |
| PWM_CLOCKA | PWMDisableMultiple() | PWMScaledClock() |
| PWM_CLOCKB | PWMDutyRead() | PWMScaler() |
| PWMActiveHigh() | PWMDutyWrite() | PWMSeparate() |
| PWMActiveLow() | PWMEnable() | PWMSetup() |
| PWMCenterAlign() | PWMEnableMultiple() | PWMUnscaledClock() |
Overview of the PWM software drivers
Most of the PWM driver functions accept a "channel_id" (channel identifier) input parameter that specifies which PWM channel the function operates on. Each 8-bit PWM channel is identified by a channel_id in the range 0 to 7 corresponding to its bit position on the PORTP output port. For example, a channel_id of 4 identifies PWM channel 4 which is available at bit PP4 on the Digital I/O Field Header on the PDQ Board. Pairs of 8-bit channels can be concatenated to form 16-bit channels, identified by the channel_id constants PWM01, PWM23, PWM45, and PWM67 in the first column of Table 9-1. Concatenation is managed by PWMConcatenate() and PWMSeparate(), as well as by PWMSetup().
The PWM_CLOCKA and PWM_CLOCKB constants identify which clock source is to be configured by the PWMScaler() and PWMPrescaler() functions. The PWMScaledClock() or PWMUnscaledClock() (or the PWMSetup()) function configures a specified PWM channel to use either the scaled or unscaled version of the applicable clock.
The PWMActiveHigh() and PWMActiveLow() functions specify the active (starting) polarity of the specified channel. The PWMCenterAlign() and PWMLeftAlign() functions determine the alignment of the specified channel. Remember that center-aligned PWM outputs have a period that is twice as long as the value written by PWMPeriodWrite().
A set of read and write operators provide visibility and control of the PWM period, duty, and counter registers. These functions are aptly named PWMPeriodRead(), PWMDutyRead(), PWMCounterRead(), PWMPeriodWrite(), PWMDutyWrite(), and PWMCounterWrite().
After a channel has been configured, it can be enabled by PWMEnable() so that its periodic output will appear on the corresponding pin. The PWMDisable() function disables a specified PWM channel so that its periodic output is stopped and is no longer driven out to the PORTP pin. If you want to enable or disable multiple PWM channels at a time, simply pass a bitmask (containing 1’s in the target channel bit positions) to the PWMEnableMultiple() or PWMDisableMultiple() functions.
Configuring the PWM clock sources
The PWM system provides four clock sources that can drive the PWM channels. The period of the clock source sets the timing resolution of the associated PWM output. For example, a PWM channel driven by a clock source with a 2 microsecond period can be configured with a period and duty (active time per period) in increments of 2 microseconds.
The two main clock sources are identified by the C constants PWM_CLOCKA and PWM_CLOCKB, and the period of each of these clocks can be varied by specifying a "prescaler". A slower "scaled" version of each of these clocks is also available; the scaled clock’s period is longer than the unscaled clock owing to a "scaler" factor that can be specified as discussed below. The scaled clocks are called SA and SB. No C-callable constants are defined to name the scaled clocks; rather, they are specified using calls to the PWMScaledClock() function.
The PWMPrescaler() routine sets the period of PWM_CLOCKA and PWM_CLOCKB to be 1, 2, 4, 8, 16, 32, 64, or 128 times the 0.05 microsecond bus clock (E-clock) period. The 20MHz frequency is reduced (the 0.05 microsecond period is increased) by the specified prescale factor. For a slower clock, use the scaled clocks SA or SB which are further slowed by a scale factor set by the PWMScaler() function. The scale factor can slow the clock by the any even integer between 2 and 512, inclusive, compared to the unscaled clock.
The 8-bit PWM channels 2, 3, 6, 7, and 16-bit channels PWM23 and PWM67 use PWM_CLOCKB or SB (scaled clockB) as their clock source.
Valid channel_id parameters for 8-bit PWM channels are in the range 0 to 7. Valid 16-bit (concatenated) channel_id constants are PWM01, PWM23, PWM45, and PWM67; concatenated outputs are available on the numerically higher PORTP channel pin mentioned in each named constant.
The PWM_CLOCKA and PWM_CLOCKB clock_id (clock identifier) constants identify which clock source is to be configured by the PWMPrescaler() and PWMScaler() functions. The PWMScaledClock() and PWMUnscaledClock() functions accept a channel_id input parameter, and configure the specified PWM channel to use either the scaled or unscaled version of the applicable clock. As explained in the next section, you can also use PWMSetup() to specify the use of a scaled or unscaled clock for a given PWM channel.
The PWMPrescaler() function accepts clock_id and prescaler input parameters to configure the period of the specified clock. The clock_id can be either PWM_CLOCKA or PWM_CLOCKB, and the prescaler can be 1, 2, 4, 8, 16, 32, 64, or 128. PWMPrescaler() applies the given prescaler factor to both the scaled and unscaled versions of the specified clock in the PWM subsystem. The fundamental clock is the 20 MHz bus clock E which has a 0.05 microsecond period, and the period is increased by the prescaler factor to create the specified PWM_CLOCKA or PWM_CLOCKB.
The PWMScaler() function accepts clock_id and scaler input parameters to configure the period of the scaled version of the specified clock. The clock_id can be either PWM_CLOCKA or PWM_CLOCKB, and the scaler can be any even integer between 2 and 512, inclusive. The default scale factor for each clock after a hardware reset is 512, meaning that by default, the scaled clockA (SA) clock is 512 times slower than PWM_CLOCKA, and the scaled clockB (SB) clock is 512 times slower than PWM_CLOCKB.
In summary, the prescale factor set by PWMPrescaler() is applied to both the scaled and unscaled versions of the specified clock. The PWMScaler() function applies a second scale factor to the specified clock to create a longer-period scaled SA and/or scaled SB. Allowed values of the prescaler are powers of 2 from 1 to 128, and allowed values of the scaler are even integers in the range 2 to 512.
Clock configuration example
Let’s assume that we want to configure the PWM channels as follows:
- Channel 0 to have a 1.6 us (microsecond) clock source, corresponding to 625 kHz, using the unscaled PWM_CLOCKA,
- Channel 1 to have a 64 us clock source, corresponding to appx. 16 kHz, using the scaled SA clock,
- Channel 2 to have a 6.4 us clock source, corresponding to appx. 156 kHz, using unscaled PWM_CLOCKB, and,
- Channels 3 and PWM67 to have a 512 us clock source, corresponding to appx. 2 kHz, using the scaled SB clock.
Recall that the fundamental bus clock (E clock) has a period of 0.05 microseconds (us). We need to calculate the prescale factors (must be powers of 2 in the range 1 to 128) by which we can multiply 0.05 us to obtain the desired unscaled clock periods for PWM_CLOCKA and PWM_CLOCKB. Then we calculate the scale factors (must be even numbers between 2 and 512) that generate the scaled versions of the clocks. We set the clock periods to the desired values by executing the following commands:
PWMPrescaler(PWM_CLOCKA, 32); // clockA period = 1.6us = 32 * 0.05us PWMScaler(PWM_CLOCKA, 40); // scaled clockA = 40 * 1.6us = 64us PWMPrescaler(PWM_CLOCKB, 128); // clockB period = 6.4us = 128 * 0.05us PWMScaler(PWM_CLOCKB, 80); // scaled clockB = 80 * 6.4us = 512us
We then specify whether each channel uses the scaled or the unscaled version of the clock. Recall that the 8-bit PWM channels 0, 1, 4, 5, and 16-bit channels PWM01 and PWM45 can be clocked by either PWM_CLOCKA or SA (a scaled version of PWM_CLOCKA). The 8-bit PWM channels 2, 3, 6, 7, and 16-bit channels PWM23 and PWM67 can be clocked by either PWM_CLOCKB or SB (a scaled version of PWM_CLOCKB).
PWMUnscaledClock(0); // pwm0 uses clockA @ 1.6us PWMScaledClock(1); // pwm1 uses SA @ 64us PWMUnscaledClock(2); // pwm2 uses clockB @ 6.4us PWMScaledClock(3); // pwm3 uses SB @ 512us PWMScaledClock(PWM67); // pwm67 uses SB @ 512us
The code statements listed above implement the clock sources as described in the example. The next section describes how to complete the configuration of one or more PWM channels using the PWMSetup() function.
The PWMSetup() function
The most versatile PWM configuration function is PWMSetup(). Its function prototype is:
void PWMSetup (int active_high, int scaled_clock, int centered, int period, int duty, int channel_id)
This function specifies the characteristics of a PWM channel having the specified channel_id (channel identifier). Valid channel_id parameters for 8-bit PWM channels are in the range 0 to 7, and the PWM output on the corresponding PORTP pin. Valid 16-bit (concatenated) channel_id constants are PWM01, PWM23, PWM45, and PWM67; concatenated outputs are available on the numerically higher PORTP channel pin mentioned in each named constant. While the period and duty cycle of an 8-bit PWM can be specified in the range 1 to 255, the period and duty cycle of a 16-bit PWM can be specified in the range 1 to 65,535, and this allows much greater resolution.
If the specified PWM channel has already been enabled when PWMSetup() is invoked, the channel is disabled during configuration to prevent anomalous transient behavior. Then the specified parameters are written to the registers, and the specified PWM channel’s enable bit is restored to the state it was in before this routine was called.
If the active_high input flag is true, the signal is configured to start in the (active) high state. If the active_high parameter is false (the default after a hardware reset), the signal is configured to start in the (active) low state. If the scaled_clock flag is true, the channel is configured to use the (slower, longer-period) scaled clock. If the scaled_clock flag is false (the default after a hardware reset), the channel is configured to use the unscaled clock. 8-bit PWM channels 0, 1, 4, 5, and 16-bit channels PWM01 and PWM45 can be clocked by either unscaled or scaled versions of PWM_CLOCKA. 8-bit PWM channels 2, 3, 6, 7, and 16-bit channels PWM23 and PWM67 can be clocked by either unscaled or scaled versions of PWM_CLOCKB.
If the centered flag input parameter is true, the PWM channel is configured to be center aligned. If the centered flag is false (the default after a hardware reset), the PWM channel is configured to be left-aligned. For standard left aligned outputs, the PWM counter register starts at 0 and counts up to the value stored in the 8- or 16-bit period register - 1, and then resets to zero to start the next cycle; as a result, the period equals the value in the 8- or 16-bit period register for standard left aligned signals. For center aligned outputs, the counter starts at 0 and counts up to the value stored in the 8- or 16-bit period register, and then counts down to zero. This symmetrical up/down counting approach ensures a center aligned signal, and it also results in an output period that is twice the value stored in the 8- or 16-bit period register. In each case, when the counter value matches the duty value, the output changes state.
The period input parameter is passed by PWMSetup() to the PWMPeriodWrite() function which stores the parameter into the period register (if the channel_id is an 8-bit PWM) or register pair (if the channel_id is a 16-bit PWM). Recall that the actual period will be double the specified period if the centered flag is true.
The duty input parameter is passed by PWMSetup() to the PWMDutyWrite() function which stores the parameter into the duty register (if the channel_id is an 8-bit PWM) or register pair (if the channel_id is a 16-bit PWM).
How to use the PWM software drivers: an C programming example
Prior sections in this chapter discussed the available driver functions, and described the clock configuration and PWMSetup() functions in detail. Briefly, we learned that the clock(s) should be configured before the specified channels are enabled. Typically, clocks are configured using the the PWMPrescaler() and PWMScaler() functions, and then PWMSetup() is called for each channel or channel pair. Finally, PWMEnable() or PWMEnableMultiple() is called to start the PWM signal(s).
The following example of use shows how to use these functions to create pulse-width-modulated outputs. Assume we want to simultaneously enable the two 8-bit channels 0 and 1 which drive the outputs PP0 and PP1 on the Digital I/O Field Header on the PDQ Board. Both are to be left aligned active high signals. PWM channel 0 is to have a 40% duty cycle with a 6.4us high time and a 16 microsecond (us) period. PWM channel 1 is to have a 60% duty cycle with a 384us high time and a 640 us period.
Since both channels 0 and 1 use the A clocks (unscaled or scaled PWM_CLOCKA), we must first configure these to facilitate the design. We’ll use the unscaled PWM_CLOCKA as the source for channel 0, and the SA (scaled PWM_CLOCKA) source for channel 1. The fundamental clock source is the E-clock with a period of 0.05 microseconds (us). We choose a prescaler of 32, resulting in an unscaled period of 1.6 us (= 0.05us * 32) for PWM_CLOCKA. This sets the minimum time resolution of a PWM channel using PWM_CLOCKA at 1.6 microseconds.
For the slower PWM channel 1 in this example, we use the SA clock (scaled PWM_CLOCKA) with a period of 64 us. We’ll specify the period of each channel as 10 counts; thus the channel 0 period is 10 * 1.6us = 16 us, and the channel 1 period is 10 * 6.4us = 64 us, as desired. The required duty cycle of channel 0 is 40%, so we specify a duty parameter of 4 (4/10 = 40%). The required duty cycle of channel 1 is 60%, so we specify a duty parameter of 6 (4/10 = 60%). For left-aligned signals, the duty parameter sets the number of clock cycles that the PWM output spends in its active state. In this example, the signals are active high, so writing a value of 4 to the channel 0 duty register will result in an active high time of 4 * 1.6us = 6.4us, which is 40% of the 16us period as desired.
Finally, to simultaneously enable the two PWM channels we note that the bitmask for the combination of channels 0 and 1 equals decimal 3; that is, a bitmask with bits 0 and 1 set has a value of 3, and this is the parameter we will pass to PWMEnableMultiple() to simultaneously enable 8-bit PWM channels 0 and 1 after PWMSetup() has executed. We assume that this example starts after a power-up or hardware reset, with all of the PWM channels initially disabled. Here is the code that fulfills the requirements of this example:
// first set the clock periods… PWMPrescaler(PWM_CLOCKA, 32); // clockA period = 1.6us PWMScaler(PWM_CLOCKA, 40); // scaled clockA = 40 * 1.6 = 64us PWMUnscaledClock(0); // PWM0 uses clockA @ 1.6us PWMScaledClock(1); // PWM1 uses SA @ 64us // now call PWMSetup() for PWM0, the next comment line recaps the prototype: // PWMSetup( active_high, scaled_clock, centered, period, duty, channel_id ) PWMSetup(TRUE, FALSE, FALSE, 10, 4, 0); // setup but don’t enable PWM0 // now call PWMSetup() for PWM1, the next comment line recaps the prototype: // PWMSetup( active_high, scaled_clock, centered, period, duty, channel_id ) PWMSetup(TRUE, TRUE, FALSE, 10, 6, 1); // setup but don’t enable PWM channel 1 PWMEnableMultiple(3); // simultaneously enable PWM channels 0 and 1
Executing this code will create PWM outputs on pins PP0 and PP1 on the Digital I/O field header.
Now let’s say you want to change the output on channel 0 from active high to active low. Simply execute:
PWMActiveLow(0); // make channel 0 active low
If you are monitoring the output with an oscilloscope, you will see the polarity of the PWM signal invert when this command is executed.
As an additional exercise, let’s say you want to double the period of channel 1 to 1280us while keeping its active high time unchanged at 384us. This means that we need to double the period register from 10 to 20, while leaving the duty value unchanged at 6. We accomplish this by executing:
PWMPeriodWrite(20, 1); // write 20 to the period register of channel 1
This example shows how the PWM control functions work together to facilitate the configuration of pulse-width modulated signals.
C language algorithms for best PWM precision
If you need very high precision it's best to configure your PWM channels as 16-bit counters so that you can have the greatest number of clock counts in a period. The PWM subsystem supports up to four 16-bit PWM counters.
Whichever counters you use, because the ON time and period take on only integer values an arbitrary ideal duty cycle can not usually be produced exactly, but only approximated. Further, the PWM precision you can attain depends on whether you choose a fixed period for your signal and vary only the ON time, or allow both the ON time and period to vary to best match an ideal duty cycle.
If you choose a fixed period and select the ON time to best approximate your ideal duty cycle, then the error between the actual duty cycle produced and the ideal is an absolute portion of full scale (100%), or,
|Dactual - Dideal| < 1/(2CP)
If you allow the period to vary and choose both the ON time and period to best match your ideal duty cycle, then the error is reduced to a relative portion of the duty cycle, or,
|Dactual - Dideal| < Dideal/(2CP)
Fixed period PWM
If your application requires that the PWM frequency remain constant as you vary the duty cycle then you must use a fixed period and vary only the ON time. You can only change the ON time in fixed integer steps, providing discrete duty cycles of 0/CP, 1/CP, 2/CP … (CP-1)/CP, and CP/CP. The period remains constant at CP counts. You get best resolution if you choose CP to be the maximum possible. For the 8-bit counters, CPmax = 255 and for the 16-bit counters CPmax = 65535.1)
To choose the ON time, you calculate,
CON = Dideal CP (rounding the operation to the nearest integer)
then
Dactual = CON / CP
and
|Dactual - Dideal| < 1/(2CP)
If you use the maximum period possible,
|Dactual - Dideal| < 1/510 ≅ 0.002 for the 8-bit counters, or,
|Dactual - Dideal| < 1/131070 ≅ 7.6E-6 for the 16-bit counters.
Variable period PWM
If your application allows it, you can vary both the period and ON time to best match your ideal duty cycle. In that case the frequency also varies. The following is a simple algorithm that allows you to choose good values for period and ON time while keeping the frequency variation to within a factor of two.
First, choose the maximum period; for example, for the 8-bit counters choose CPmax = 255. We'll then allow the actual period to vary between one half of the maximum and the full maximum.
To choose the ON time, calculate,
CON = Dideal CPmax (rounding the operation to the smallest integer)
then choose the period as,
CP = CON / Dideal (rounding the operation to the nearest integer)
Then, the actual duty cycle produced is,
Dactual = CON / CP
and
|Dactual - Dideal| < Dideal/(2CP) < Dideal/(CPmax)
If you use the maximum period possible,
|Dactual - Dideal| < Dideal/255 ≅ 0.004 Dideal for the 8-bit counters, or,
|Dactual - Dideal| < Dideal/655350 ≅ 1.56E-5 Dideal for the 16-bit counters.
Using this method you can produce very fine resolution. In particular, at the low end, for small duty cycle, the duty cycle can still be very finely adjusted, to within one part in CPmax of its value. Even so, the smallest duty cycle attainable is 1/CPmax; there is a gap between 0 and 1/CPmax where no duty cycle values can be produced. The greatest turn down is a factor of CPmax.
Choosing clock frequencies for multiple channels
You can choose to clock PWM channels 0, 1, 4, or 5 from either PWM_CLOCKA with a frequency of
fA = f0 / FPSA
or clock SA with a frequency of
fSA = f0 / (FPSA FSA)
where,
the prescale factor, FPSA, is chosen from a powers of two (1, 2, 4, 8, 16, 32, 64, or 128); and,
the scale factor, FSA, is chosen as an even integers from 2 to 512 (2, 4, 6, 8, … 510, or 512).
Similarly, channels 2, 3, 6, and 7 are clocked from PWM_CLOCKB or SB.
The following table shows the range in clock frequencies available for different prescale (FPS) and scale (FS) factors. The clock frequencies (in green) are rounded to the nearest Hz:
| Clock Frequencies (kHz) for various prescale (FPS) and scale (FS) factors | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Prescale factor | Scale factor, FSA or FSB | ||||||||
| FPSA/B | PWM_CLOCKA/B | FS= 2 | FS= 4 | FS= 6 | FS= 8 | FS= 10 | … | FS=510 | FS=512 |
| 1 | 20000.000 | 10000.000 | 5000.000 | 3333.333 | 2500.000 | 2000.000 | … | 39.216 | 39.063 |
| 2 | 10000.000 | 5000.000 | 2500.000 | 1666.667 | 1250.000 | 1000.000 | … | 19.608 | 19.531 |
| 4 | 5000.000 | 2500.000 | 1250.000 | 833.333 | 625.000 | 500.000 | … | 9.804 | 9.766 |
| 8 | 2500.000 | 1250.000 | 625.000 | 416.667 | 312.500 | 250.000 | … | 4.902 | 4.883 |
| 16 | 1250.000 | 625.000 | 312.500 | 208.333 | 156.250 | 125.000 | … | 2.451 | 2.441 |
| 32 | 625.000 | 312.500 | 156.250 | 104.167 | 78.125 | 62.500 | … | 1.225 | 1.221 |
| 64 | 312.500 | 156.250 | 78.125 | 52.083 | 39.063 | 31.250 | … | 0.613 | 0.610 |
| 128 | 156.250 | 78.125 | 39.063 | 26.042 | 19.531 | 15.625 | … | 0.306 | 0.305 |
Using the prescaler alone, clock frequencies in factors of two from 20MHz to 156.25 kHz can be used. Using the scaled clock, clock frequencies down to 305Hz are possible. Keep in mind that these are the clock frequencies, not the frequency of the PWM outputs. The output frequencies are the clock frequency used divided by the PWM periods. Consequently, for the 8-bit counters, you can divide the frequencies of the above table by periods from 2 to 255, to get PWM frequencies down to 1.2Hz. If you concatenate channels to use 16-bit counters, you can divide the frequencies of the above table by periods from 2 to 65535, to get PWM frequencies down to 0.00466Hz, or PWM periods as long as several minutes.
For quick reference, the following tables show the PWM output frequencies in Hz (in green) as a function of the prescale and scale factors, assuming that the PWM period is set to its maximum of 255 for 8-bit counters or 65535 for the concatenated 16-bit counters.
| PWM Output Frequencies (Hz) when CP=255 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Prescale factor | Scale factor, FSA or FSB | ||||||||
| FPSA/B | PWM_CLOCKA/B | FS= 2 | FS= 4 | FS= 6 | FS= 8 | FS= 10 | … | FS=510 | FS=512 |
| 1 | 78431 | 39216 | 19608 | 13072 | 9804 | 7843 | … | 154 | 153 |
| 2 | 39216 | 19608 | 9804 | 6536 | 4902 | 3922 | … | 76.9 | 76.6 |
| 4 | 19608 | 9804 | 4902 | 3268 | 2451 | 1961 | … | 38.4 | 38.3 |
| 8 | 9804 | 4902 | 2451 | 1634 | 1225 | 980 | … | 19.2 | 19.1 |
| 16 | 4902 | 2451 | 1225 | 817 | 613 | 490 | … | 9.61 | 9.57 |
| 32 | 2451 | 1225 | 613 | 408 | 306 | 245 | … | 4.81 | 4.79 |
| 64 | 1225 | 613 | 306 | 204 | 153 | 123 | … | 2.40 | 2.39 |
| 128 | 613 | 306 | 153 | 102 | 76.6 | 61.3 | … | 1.20 | 1.20 |
| PWM Output Frequencies (Hz) when CP=65535 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Prescale factor | Scale factor, FSA or FSB | ||||||||
| FPSA/B | PWM_CLOCKA/B | FS= 2 | FS= 4 | FS= 6 | FS= 8 | FS= 10 | … | FS=510 | FS=512 |
| 1 | 305.180 | 152.590 | 76.295 | 50.863 | 38.148 | 30.518 | … | 0.598 | 0.596 |
| 2 | 152.590 | 76.295 | 38.148 | 25.432 | 19.074 | 15.259 | … | 0.299 | 0.298 |
| 4 | 76.295 | 38.148 | 19.074 | 12.716 | 9.537 | 7.630 | … | 0.150 | 0.149 |
| 8 | 38.148 | 19.074 | 9.537 | 6.358 | 4.768 | 3.815 | … | 0.0748 | 0.0745 |
| 16 | 19.074 | 9.537 | 4.768 | 3.179 | 2.384 | 1.907 | … | 0.0374 | 0.0373 |
| 32 | 9.537 | 4.768 | 2.384 | 1.589 | 1.192 | 0.954 | … | 0.0187 | 0.0186 |
| 64 | 4.768 | 2.384 | 1.192 | 0.795 | 0.596 | 0.477 | … | 0.00935 | 0.00931 |
| 128 | 2.384 | 1.192 | 0.596 | 0.397 | 0.298 | 0.238 | … | 0.00467 | 0.00466 |
For convenience in the following discussion we'll shorten the above expressions for the clock frequency to a channel independent form (with the understanding that the more specific expressions are actually used for specific channels):
fc = f0 / (FPS FS)
where,
fc = the channel clock frequency,
f0 = the 20MHz master clock frequency,
FPS is a prescale factor chosen from [1, 2, 4, 8, 16, 32, 64, or 128], and,
the scale factor FS = 1 or it is chosen from [2, 4, 6, 8, 10, … 508, 510, or 512].
In the above expression, the value FS = 1 is intended to represent the choice to use PWM_CLOCKA/PWM_CLOCKB instead of SA/SB for the clock source.
The PWM frequency produced by a channel is the channel's clock frequency divided by its period (in clock counts), as,
fPWM = f0 / (FPS FS CP)
The frequency is determined by three parameters. The prescale factor, which can be set only to the nearest power of two, is used for coarse frequency setting. The scale factor, with a resolution afforded by even integers, provides finer frequency settings. Finally, we can choose a period to set the frequency with very fine resolution.
We see that we have great flexibility in choosing values of the scale factors, FPS and FS, and the period, CP. These factors are partially redundant; different sets of values can produce the same PWM frequency.
If we are using only one or two channels we have complete freedom in choosing values for these three parameters. However, if we use more channels then we are constrained in our choice owing to the partially overlapping scope of the parameters. The prescale and scale factors apply to an entire set of four channels; each channel can use either the prescaled clock or the prescaled and scaled clock; and the period may be chosen independently for each channel.
How these parameters are chosen will depend on the needs of the application. Some applications require that the frequency be set with the greatest precision possible, while others will give duty cycle resolution the highest priority.
Channel sets A (1,2,4, and 5) and B (2,3,6, and 7) are completely independent, so to produce widely spaced frequencies we can serve the high frequencies from one set and the low frequencies from the other, with complete freedom in choosing the prescale and scale factors for each.
It's trickier to choose prescale and scale factors for multiple frequencies produced within a channel set. Let's see how we should pick the scale factors to produce several frequencies, f1 < f2 < f3 < f4 on several channels within a group of four. We'll consider two cases, for closely spaced frequencies and for widely spaced frequencies.
Producing closely spaced frequencies
As a rule of thumb, if the total span of frequencies is less than a factor of two, then we will use the same clock source for all channels, and adjust the frequency by adjusting CP. In that case, we choose FPS and FS to provide a PWM frequency equal to or just less than the lowest frequency desired when CP=CPmax. That is, we choose FPS and FS so that for 8-bit channels,
FPS FS ≥ f0 / (f1 CPmax) = 20MHz /(f1 * 255)
Then to set each of the output frequencies for each of the channels (i=1,2,4,5 for channel set A or i=2,3,6,7 for channel set B) we compute,
CPi = f0 / (fi FPS FS)
Producing widely spaced frequencies
If the total span of frequencies is greater than a factor of two, then we will need to use both clock sources for the channels. If the highest frequencies are close together, so that their difference can be easily spanned by minor adjustments in CP, then the lowest of those high frequencies is used to choose FPS assuming CP=CPmax and selecting the prescaled clock for those channels. If the highest frequency stands out by being more than a factor of two greater than the rest2), then it is used to choose FPS, as,
FPS ≥ f0 / (fhighest CPmax)
The individual frequencies of the set of high frequencies are then produced by optimizing CP for each channel, as,
CPi = f0 / (fi FPS)
Once FPS is chosen, we then select FS based on the lowest frequency channel. It is chosen as,
FS ≥ f0 / (flowest FPS CPmax)
The individual frequencies of the low frequency set are then produced by optimizing CP for each channel and driving the channel with the prescaled and scaled clock, as,
CPi = f0 / (fi FPS FS)
Precise frequency generation
The above sections focused on creating precise duty cycles in a PWM waveform. But often, you need precise frequency generation rather than duty cycle generation. Here we'll discuss how to generate a precise frequency of nearly 50% duty cycle.
The PWM subsystem creates an output frequency by dividing the 20 MHz clock frequency by three factors, as,
fout = f0 / (FPS FS CP)
where,
fout is the channel output frequency,
f0 is the 20MHz master clock frequency,
CP is the period of the waveform, chosen from [2, 4, 6, 8, … 65534] for even 16-bit periods,
FPS is the prescale factor chosen from [1, 2, 4, 8, 16, 32, 64, or 128], and,
the scale factor FS = 1 or it is chosen from [2, 4, 6, 8, 10, … 508, 510, or 512].
The greatest resolution is attained by using a 16-bit rather than an 8-bit period. Further, in the above expression, the value FS = 1 is intended to represent the choice to use PWM_CLOCKA/PWM_CLOCKB instead of SA/SB for the clock source.
The frequency is determined by three parameters. The prescale factor, which can be set only to the nearest power of two, is used for coarse frequency setting. The scale factor, with a resolution afforded by even integers, provides finer frequency settings. Finally, we can choose a period to set the frequency with very fine resolution. In particular, if we use a 16-bit period, when the period is a number near the upper end of its range it can be adjusted with fine relative precision.
Using the above equation, the frequency range available is approximately 0.00465668 Hz (one cycle per 215 seconds) to 10 Mhz.
We have great flexibility in choosing values of the scale factors, FPS and FS, and the period, CP. These factors are partially redundant; different sets of values can produce the same PWM frequency. Because we want to generate a frequency as accurately as possible, we should choose the various scale factors to keep the scale factors with the greatest resolution near the top end of their range. Consequently, the algorithm should give precedence first to using large values of the period, then to large values of the scale factor, while the prescale factor provides only coarse adjustment.
This following routine implements such an algorithm, finding the parameters to send to the PWM subsystem to produce a frequency with nearly 50% duty cycle that best matches a desired frequency. The actual frequency is highly accurate, and derives its accuracy from the master clock at 20 MHz (±100ppm). For half of the attainable frequencies the duty cycle produced is exactly 50% (for even periods) while for the other half (with odd periods) the duty cycle is nearly 50%, with the ON time just one clock pulse briefer than the OFF time. The worst case error between the desired frequency and the actual frequency is less than one part in 217 for frequencies up to 80 Hz, one part in 216 up to 610 Hz, better than 0.1% at up to 40 kHz, and better than 1% at up to 400kHz. For frequencies less than 305 Hz, for most input values the matching of produced frequency to desired frequency is actually much better — by a large factor – only for relatively rare values is the resolution near the worst case.
The logic of the algorithm is as follows:
For a desired frequency greater than 305.2Hz (20MHz/65535.5), the prescale and scale factors are unity and only the period is adjusted to match the frequency, as,
P = f0 / fdesired rounded to the nearest integer.
For a desired frequency between 152.6 Hz and 305.2Hz, the scale factor is set to 2 and the period is adjusted to match the frequency, as,
P = f0 / (2⋅fdesired) rounded to the nearest integer.
For lower frequencies the prescale factor is chosen to maximize the period and the best combination of period and scale factor is chosen by inspecting all possible combinations and using the one that best matches the desired frequency.
- First, the prescale factor, FPS, is set to the smallest power of two that keeps P = f0/(512⋅fdesired⋅FPS) ≤ 65535
- Then, we find the best scale factor, computing the best period for each scale factor, so that the combination of scale factor and period results in a frequency that best matches the desired frequency. To do so, we examine all scale factors, and choose the best. We usually don't need to examine all 257 possible values of scale factor, but only those even integers between 2 and 512 and also in the range of f0/(fdesired⋅FPS⋅65535) and f0/(fdesired⋅FPS).
The following listing provides a Forth language implementation of the above algorithm:
1: 1 WRITE.ENABLE \ Needed to assure that we can write to the code area on page 0x00 2: 2 WRITE.ENABLE \ Needed to assure that we can write to the names area on page 0x10 3: DEFAULT.MAP \ Places the dictionary (code) and names on pages 00 and 10 respectively 4: 5: ANEW FreqGenerator 6: 7: \ This program uses the PWM subsystem as a frequency generator. All frequencies are 8: \ produced using identical ON and OFF times, so the duty cycle deviates from an ideal 9: \ 50% only by whatever deviation is caused by the clock jitter on the 20MHz clock, which 10: \ should be very small. 11: 12: DECIMAL 13: 120 CHARS/LINE ! 14: 15: \ 0x0101 CONSTANT PWM01 \ 0 is msbyte, pwm1 registers control it, on pwm1 pin 16: \ 0x0103 CONSTANT PWM23 \ 2 is msbyte, pwm3 registers control it, on pwm3 pin 17: \ 0x0105 CONSTANT PWM45 \ 4 is msbyte, pwm5 registers control it, on pwm5 pin 18: \ 0x0107 CONSTANT PWM67 \ 6 is msbyte, pwm7 registers control it, on pwm7 pin 19: \ 0xA8 CONSTANT PWM.CLOCKA \ The address (not the value) of PWMSCLA 20: \ 0xA9 CONSTANT PWM.CLOCKB \ The address (not the value) of PWMSCLB 21: 22: 23: 24: 20E6 FCONSTANT MasterClock \ 20MHz system clock 25: 4.65668E-3 FCONSTANT MinFrequency \ The minimum frequency that can be produced 26: 10E6 FCONSTANT MaxFrequency \ The maximum frequency that can be produced 27: MasterClock 65535.5 F/ FDUP FCONSTANT FTopRange F2/ FCONSTANT FNextRange 28: \ Frequencies above FTopRange are produced with Fps=Fs=1 and periods from 2 to 65535 29: \ Frequencies between FNextRange and FTopRange use Fps=1 Fs=2 and P=32767 to 65535 30: 31: : FindParameters ( Frequency -- Fps\Fs\P\Factual ) 32: \ This routine finds the parameters to send to the PWM subsystem to produce 33: \ a frequency with nearly 50% duty cycle that best matches the desired frequency. 34: \ The best possible combination of prescale factor, Fps, scale factor, Fs, and period, 35: \ P, are found to most closely match the desired frequency. Those factors are returned, 36: \ along with the actual frequency produced. The actual frequency is highly accurate, 37: \ and derives its accuracy from the master clock at 20 MHz (±100ppm). 38: \ For half of the attainable frequencies the duty cycle produced is exactly 50% (for 39: \ even periods) while for the other half (with odd periods) the duty cycle is nearly 40: \ 50%, with the ON time just one clock pulse briefer than the OFF time. Frequencies 41: \ may be produced in the range of 0.00465668 Hz (one cycle per 215 seconds) 42: \ to 10 MHz. The worst case error between the desired frequency and the actual 43: \ frequency is less than one part in 2^17 for frequencies up to 80Hz 44: \ 90 Hz, one part in 2^16 up to 610 Hz, better than 0.1% at up to 40 kHz, and 45: \ better than 1% at up to 400kHz. For frequencies less than 305 Hz, for most input 46: \ values the matching of produced frequency to desired frequency is actually much 47: \ better --- by a large factor -- only for relatively rare values is the resolution 48: \ near the worst case. 49: \ The input, Frequency, is the desired frequency as a floating point number 50: \ Fps, Fs and P are 16-bit unsigned integers for the prescale factor, scale factor 51: \ and period. Factual is the actual frequency produced, as a floating point number. 52: MinFrequency FMAX MaxFrequency FMIN 53: Locals{ F&frequency | &Fps &Fs F&FpsFs F&Product &P F&error &bestP &testFs F&testFs } 54: F&frequency FTopRange F>= \ frequencies greater than about 305.2Hz 55: IF \ For these high frequencies, the prescale and scale factors are unity, and the 56: \ period varies from 2 (for 10 MHz) to 65535 (for 305 Hz) 57: \ P=Fo/f rounded to the nearest integer 58: 1 1 MasterClock F&frequency F/ UFIXX DUP UFLOT MasterClock FSWAP F/ 59: ELSE 60: F&frequency FNextRange F>= \ frequencies greater than about 152.6 Hz 61: IF \ For frequency between 153 and 305 Hz the prescale factor = 1 and scale factor 62: \ = 2 while the period varies from 32767 to 65535 63: \ P=Fo/2f rounded to the nearest integer 64: 1 2 MasterClock F&frequency F/ F2/ UFIXX DUP UFLOT MasterClock FSWAP F/ F2/ 65: ELSE 66: \ For lower frequencies the prescale factor is chosen to maximize the period and the 67: \ best combination of period and scale factor is chosen by inspecting all possible 68: \ combinations and using the one that best provides the desired frequency. 69: MasterClock F&frequency F/ 65535. F/ TO F&FpsFs 70: F&FpsFs 512. F<= IF 1 ELSE F&FpsFs 1024. F<= IF 2 ELSE 71: F&FpsFs 2048. F<= IF 4 ELSE F&FpsFs 4096. F<= IF 8 ELSE 72: F&FpsFs 8182. F<= IF 16 ELSE F&FpsFs 16384. F<= IF 32 ELSE 73: F&FpsFs 32768. F<= IF 64 ELSE 128 74: ENDIF ENDIF ENDIF ENDIF ENDIF ENDIF ENDIF TO &Fps 75: \ Now that we have the prescale factor, Fps, we want to find the best combination of 76: \ scale factor, Fs, and period, P, so that their product best matches the desired 77: \ product. To do so we examine all combinations (there are a maximum of 257 78: \ combinations to try), but we usually don't have to try them all. 79: MasterClock &Fps FLOT F/ F&frequency F/ TO F&Product 80: F&Product FABS TO F&error 81: \ the max loop index: 82: F&Product F2/ 1.0 F+ FLOOR F2* 512. FMIN 0. FMAX FIXX 2+ 83: \ the min loop index: 84: F&Product 65535. F/ F2/ FLOOR F2* 512. FMIN 0. FMAX FIXX 85: DO 86: I 0= IF 1 ELSE I ENDIF DUP TO &testFs FLOT TO F&testFs 87: F&Product F&testFs F/ UFIXX 2 UMAX 65535 UMIN DUP TO &P 88: UFLOT F&testFs F* F&Product F- FABS FDUP F&error F< 89: IF TO F&error &testFs TO &Fs &P TO &bestP 90: ELSE FDROP 91: ENDIF 92: 2 +LOOP 93: &Fps &Fs &bestP 94: MasterClock &bestP UFLOT F/ &Fs FLOT F/ &Fps FLOT F/ 95: ENDIF 96: ENDIF 97: ; 98: 99: : FrequencyOut ( Frequency\channelID -- Factual ) 100: \ Frequency is the desired frequency in Hz as a floating point number and channelID 101: \ is an interger representing the 16-bit PWM channel to use. Factual is the actual 102: \ frequency produced, as a floating point number. 103: \ This routine configures the PWM subsytem to produce an output frequency with nearly 104: \ 50% duty cycle. The 16-bit, high resolution PWM channels must be used, so valid 105: \ channelID numbers are PWM01, PMW23, PWM45, or PWM67 106: FALSE Locals{ &Scaled &channelID F&frequency | F&Factual &Fps &Fs &P &AorB } 107: F&frequency FindParameters TO F&Factual TO &P TO &Fs TO &Fps 108: &channelID PWM01 = &channelID PWM45 = OR IF PWM.CLOCKA ELSE PWM.CLOCKB ENDIF TO &AorB 109: &AorB &Fps PWM.PRESCALER 110: &Fs 1 = NOT 111: IF 112: &AorB &Fs PWM.SCALER 113: TRUE TO &Scaled 114: ENDIF 115: TRUE &Scaled FALSE &P &P 2 U/ &channelID PWM.SETUP 116: &channelID PWM.ENABLE 117: F&Factual 118: ; 119: 120: : Testit 121: 8 mantissa.places ! 122: BEGIN 123: 1.0 \ Initial frequency 124: 71 0 125: DO 126: PAUSE.ON.KEY 127: FDUP PWM01 FrequencyOut CR F. 128: 10. 0.1 F** F* 129: 143 0 DO 1000 MICROSEC.DELAY LOOP 130: LOOP 131: FDROP 132: AGAIN 133: ; 134: 135: : T PWM01 FrequencyOut F. ; 136: 137: 138: SAVE 139: \ AUTOSTART: AutoTest 140: 141: 0 1 STORE.PAGES DROP \ store code page 0x00 in shadow flash 142: 0x10 1 STORE.PAGES DROP \ store names page 0x10 in shadow flash 143: \ AUTOSTART already wrote to onchip flash; no need to store it anywhere else 144: 1 WRITE.PROTECT \ protect pages 0-0xF 145: 2 WRITE.PROTECT \ protect pages 0x10-0x13 146: 0x00 1 1 LOAD.PAGES.AT.STARTUP \ load code page 0x00 to RAM at startup 147: 0x10 1 2 LOAD.PAGES.AT.STARTUP \ load names page 0x10 to RAM at startup
See also → Timer-Controlled I/O